$R$ અવરોધ અને ત્રિજ્યા $r$ ધરાવતતા એક તારને ત્યાં સુધી ખૅંયવામાં આવ છે કે જ્યાં સુધી ત્રિજ્યા $(r / 2)$ થાય. જો ખેયાયેલા તારનો નવો અવરોધ $x R$ છે. તો $x=$ . . . . . થશે.
JEE MAIN 2024, Diffcult
b
We know \(\mathrm{R}=\frac{\rho l}{\mathrm{~A}}, \mathrm{R} \propto \frac{l}{\mathrm{r}^2}\)
We know \(\mathrm{R}=\frac{\rho l}{\mathrm{~A}}, \mathrm{R} \propto \frac{l}{\mathrm{r}^2}\)
As we starch the wire, its length will increase but its radius will decrease keeping the volume constant
\(\mathrm{V}_{\mathrm{i}}=\mathrm{V}_{\mathrm{f}}\)
\(\pi^2 l=\pi \frac{\mathrm{r}^2}{4} l_{\mathrm{f}}\)
\(l_{\mathrm{f}}=4 l\)
\(\frac{\mathrm{R}_{\text {nelv }}}{\mathrm{R}_{\text {old }}}=\left(\frac{4 l}{\frac{\mathrm{r}^2}{4}}\right) \frac{\mathrm{r}^2}{l}=16\)
\(\mathrm{R}_{\text {neer }}=16 \mathrm{R}\)
\(\therefore \mathrm{x}=16\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2 \,\Omega $ અવરોધ ધરાવતા એમિટર $100\,mA $ માપી શકે છે.હવે, $5 \,V $ માપે તેવું બનાવવા માટે કેટલા ........... $\Omega$ અવરોધ શ્રેણીમાં જોડવો પડે?View Solution
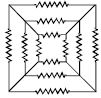
- 2બધા અવરોધનું મૂલ્ય $16 \,\Omega $ છે,તો બહારની ચોરસની એક બાજુ વચ્ચે સમતુલ્ય અવરોધ ......... $\Omega$View Solution
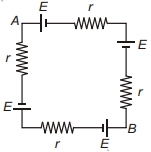
- 3દર્શાવેલ પરિપથમાં $A B$ વચ્ચે વિદ્યુતસ્થિતિમાનનો તફાવત કેટલો છે.View Solution
- 4પ્લેટીયર અચળાંક $2\times 10^{-9} \,volts$ છે.જયારે $2.5 \,amp $ પ્રવાહ $2 \,minute $ માટે પસાર કરતાં કેટલા ................. $ergs$ ઉષ્મા ઉત્પન્ન થાય?View Solution
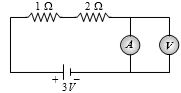
- 5આપેલ પરિપથ માટે વોલ્ટમીટરનું અવલોકન કેટલા ............ $volt$ હશે?View Solution
- 6એક કોષ $2\, \Omega$ ના અવરોધમાંથી $0.9\,\ A$ પ્રવાહ અને $7\,\Omega$ ના અવરોધમાંથી $0.3\,\ A$ પ્રવાહ પસાર કરે છે. તો કોષનો આંતરિક અવરોધ .............. $\Omega$ છે.View Solution
- 7એક પોલા નળાકાર વાહકની લંબાઇ $3.14\,m$ છે જ્યારે તેની આંતરિક અને બાહ્ય વ્યાસ અનુક્રમે $4\,mm$ અને $8\,mm$ છે.વાહકનો અવરોધ $n \times 10^{-3}\,\Omega$ છે.જો દ્રાવ્યની અવરોધકતા $2.4 \times 10^{-8}\,\Omega m$ હોય તો $n$ નું મૂલ્ય $............$ છે.View Solution
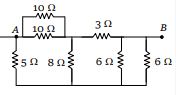
- 8આપેલ તંત્રમાં $A$ અને $B$ વચ્ચેનો સમતુલ્ય અવરોઘ કેટલા ............. $\Omega$ થાય?View Solution
- 9View Solutionએક પ્રયોગમાં બેટરીના બે છેડા વચ્ચેના વિધુતસ્થીતિમાનના તફાવત વિરુદ્ધ પરીપથના પ્રવાહનો આલેખ દોરવામાં આવે છે. તો બેટરીનો આંતરીક વાહકત્વ .... હશે.
- 10$2\,mm \times 2\,mm \times 5\,m$ પરિમાણો ધરાવત્તl કોપરના લંબચોરસ બ્લોકોની બે ચોરસ બાજુઓ વચ્ચેનું અવરોધ $0.02\,\Omega$ છે. તો કોપરની અવરોધકતા કેટલી છે?View Solution
