$R$ અવરોધ ધરાવતા ચાર અવરોધોને વ્હીસ્ટન બ્રિજની ચાર ભુજાઓમાં જોડેલા છે. જો ગેલ્વેનોમિટરની ભુજાનો અવરોધ પણ $R$ હોય, તો બેટરીને અનુલક્ષીને સમતુલ્ય અવરોધ કેટલો થાય?
AIPMT 2003, Easy
b
(b) As bridge is in balanced condition, no current will flow through \(BD.\)
(b) As bridge is in balanced condition, no current will flow through \(BD.\)
\(R_{1}=R_{A B}+R_{B C}\)
\(=R+R=2 R\)
\(R_{2}=R_{A D}+R_{C D}=R+R=2 R\)
Also, \(R_{1}\) and \(R_{2}\) are in parallel combination
Hence, equivalent resistance between \(A\) and \(C\) will be
\(R_{e q}=\frac{R_{1} R_{2}}{R_{1}+R_{2}}=\frac{4 R^{2}}{4 R}=R\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે ઇલેક્ટ્રિક બલ્બો કે જેનું અવરોધનો ગુણોતર $1:2$ છે. તેમને અચળ વૉલ્ટેજ ઉદગમ સાથે સમાંતર જોડેલ છે. તેમનામાં થતો પાવર વ્યયનો ગુણોતર કેટલો હોય શકે?View Solution
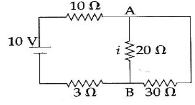
- 2આકૃતિમાં દર્શાવેલ વિદ્યુત પરિપથમાં $AB$ બાજુમાંથી વહેતો પ્રવાહ $i $ કેટલો હશે?View Solution
- 3કોપરના તારના દળનો ગુણોત્તર $1 : 3 : 5 $ અને તેની લંબાઇનો ગુણોત્તર $5 : 3 : 1 $ હોય, તો અવરોધનો ગુણોત્તર કેટલો થાય?View Solution
- 4$1.5\,V$ ના બે કોષોને $10\,\Omega$ ના અવરોધની સમાંતર શ્રેણીમાં જોડવામાં આવે છે. એક આદર્શ વોલ્ટમીટરને $10\, \Omega$ અવરોધની આસપાસ જોડતાં $1.5\,V$ નોંધે છે. દરેક કોષનો આંતરિક અવરોધ ........ $\Omega$ છે.View Solution
- 5બે સમાન $emf$ ધરાવતા પરંતુ જુદો જુદો $r_{1}$ અને $r_{2}$ આંતરિક અવરોધ ધરાવતા બે કોષોને અવરોધ $R$ સાથે શ્રેણીમાં જોડવામાં આવેલાં છે. જેનાં માટે બીજા કોષને સમાંતર સ્થિતિમાનનો તફાવત શૂન્ય થાય તે અવરોધ $R$ નું મૂલ્ચ .......થશે.View Solution
- 6$A$ અને $B$ દ્રવ્યમાંથી $B$ દ્રવ્યની અવરોધકતા $A$ કરતાં બમણી છે. $B$ દ્રવ્યમાંથી બનેલા વર્તુળાકાર તારનો વ્યાસ $A$ તાર કરતાં બમણો છે. જો બંને તારના અવરોધ સમાન બને તે માટે બંને તારની લંબાઈઓનો ગુણોત્તર $\frac{{{l_B}}}{{{l_A}}}$ કેટલો હોવો જોઈએ?View Solution
- 7$E \;e.m.f.$ ની અને $R $ આંતરિક અવરોધ ધરાવતી એક બેટરી સાથે જે દરેકનું મૂલ્ય $ R$ છે, તેવા $n$ સરળ અવરાધો શ્રેણીમાં જોડેલ છે. બેટરીથી લીધેલો પ્રવાહ $I $ છે. હવે આ $n$ અવરોધોને આ બેટરી સાથે સમાંતર જોડવામાં આવે છે. ત્યારે બેટરીથી લીધેલો પ્રવાહ $10I $ હોય છે. $n$ નું મૂલ્ય કેટલું હશે?View Solution
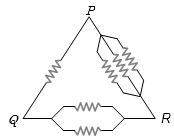
- 8View Solutionસમાન અવરોધ ધરાવતી આકૃતિમાં મહત્તમ અવરોધ કોના વચ્ચે હશે?
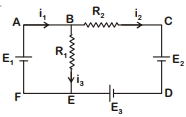
- 9આપેલ પરિપથ માટે લૂપ $BCDEB$ માટે કિચોર્ફનો નિયમ લગાવતા સમીકરણ .............. મુજબ મળેView Solution
- 10$10\, m$ લંબાઈ અને $20\, \Omega$ નો અવરોધ ધરાવતો એક પોટેન્શીયોમીટર તારને $25 \,V$ ની બેટરી અને $30\, \Omega$ ના બાહ્ય અવરોધ સાથે જોડવામાં આવે છે. $E$ જેટલું $emf$ ધરાવતા કોષને ગૌણ પરિપથમાં જોડતાં પોટેન્શીયોમીટર તાર પર $250\, cm$ લંબાઈ આગળ સંતુલન બિંદુ મળે છે. $E$ નું મૂલ્ય $\frac{x}{10} V$ છે. $x$ નું મૂલ્ય ........થશે.View Solution
