$r$ ત્રિજ્યા ધરાવતી અને $I$ પ્રવાહધારીત રીંગનાં કેન્દ્રથી $R$ અંતરે ચુંબકીયક્ષેત્ર કેટલું થશે?
AIIMS 2007, Medium
b
The magnetic field is \(B = \frac{{{\mu _0}I{r^2}}}{{2{{({R^2} + {r^2})}^{\frac{3}{2}}}}}\)
The magnetic field is \(B = \frac{{{\mu _0}I{r^2}}}{{2{{({R^2} + {r^2})}^{\frac{3}{2}}}}}\)
(see application of Biot-Savart law to magnetic field at a point along axis of coil)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$30$ કાપા ધરાવતા ગેલ્વેનોમીટરની વિધુતપ્રવાહ સંવેદીતા $20$ $\mu A$ કાપા. ક્રમની છે. તેનો અવરોધ $25\,\Omega$ નો છે. આ એમિટરને $1$ વોલ્ટના વોલ્ટમીટર કેવી રીતે ફેરવશો ............. $\Omega$View Solution
- 2એક ચલિત ગૂંચળું ધરાવતા ગેલ્વેનોમીટરમાં $100$ આંટા અને દરેક આંટાને $2.0 \mathrm{~cm}^2$ નું ક્ષેત્રફળ છે. ચુંબક દ્વારા ઉત્પન્ન ચુંબકીય ક્ષેત્ર $0.01 \mathrm{~T}$છે અને જ્યારે તેમાંથી $10 \mathrm{~mA}$ પ્રવાહ પસાર થાય છે ત્યારે ગૂંચળાનું કોણાવર્તન $0.05$ $radian$ મળે છે. ગેલ્વેનોમીટરમાં લટકાવેલ તાર માટે બળ અચળાંક $x \times 10^{-5} \mathrm{~N}-\mathrm{m} / \mathrm{rad}$ છે. $x$ નું મૂલ્ય__________છે.View Solution
- 3વર્તુળાકાર આડછેદ અને સ્થિત વિદ્યુતપ્રવાહ ઘરાવતા લાંબા સીધા તાર માટના એમ્પિયર પરિપથીય નિયમ $(circuital\, law)$ થી તારના અંદરના અને બહારના વિસ્તારમાં ચુંબકીય ક્ષેત્રનો ફેરફાર$.....$View Solution
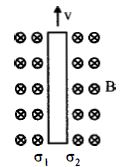
- 4એક પાતળી ધાતુની પટ્ટી કાગળના સમતલને લંબ $v$ વેગથી ગતિ કરે છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે ચુંબકીયક્ષેત્ર $B$ કાગળના સમતલની અંદરની દિશામાં પ્રવર્તે છે.જો પટ્ટીની ડાબી અને જમણી સપાટી પર પ્રેરિત થતી વિજભારઘનતા ${\sigma _1}$ અને ${\sigma _2}$ હોય તો..... (ફ્રિન્જ અસરને અવગણો)View Solution
- 5$40\, cm$ લંબાઇ ધરાવતા તારમાંથી $3\,A $ પ્રવાહ પસાર કરીને $500$ ગોસ ચુંબકીયક્ષેત્ર સાથે $ 30^\circ $ ના ખૂણે મૂકતાં તેના પર કેટલું બળ લાગે?View Solution
- 6$R$ ત્રિજ્યાની અવાહક તકતી પર $Q$ વિદ્યુતભાર નિયમિત રીતે વહેંચાયેલો છે. તકતીના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબરૂપે રહેલી અક્ષને અનુલક્ષીને તકતી $\omega$ જેટલી કોણીય ઝડપથી પરિભ્રમણ કરે છે. જેને કરાણે તકતીના કેન્દ્ર પર $B$ જેટલું ચુંબકીય ક્ષેત્ર પ્રેરિત થાય છે. હવે જે વિદ્યુતભાર અને કોણીય ઝડપને અચળ રાખીએ અને તકતીની ત્રિજ્યાને બદલાતી લઈએ તો તક્તીના કેન્દ્રમાં ચુંબકીય પ્રેરણ નીચેના પૈકી કઈ આકૃતિ પ્રમાણે બદલાશે?View Solution
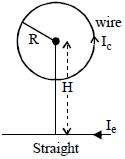
- 7વર્તુળાકાર લૂપ અને સુરેખ તારમાંથી પ્રવાહ $I_c$ અને $I_e$ પસાર થાય છે,બંને એક જ સમતલમાં છે,તો લૂપના કેન્દ્ર પર ચુંબકીય ક્ષેત્ર શૂન્ય કરવા માટે બંન્ને વચ્ચેનું અંતર $H$ ....... .View Solution
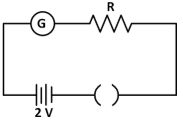
- 8એક ગેલ્વેનોમીટરમાં $50$ કાંપા છે.બેટરીનો આંતરિક અવરોધ શૂન્ય છે. જ્યારે $R = 2400\,\Omega $ જોડેલો હોય ત્યારે ગેલ્વેનોમીટર $40$ કાંપા જેટલું આવર્તન દર્શાવે છે. જ્યારે $R = 4900\,\Omega $ જોડેલો હોય ત્યારે ગેલ્વેનોમીટર $20$ કાંપા જેટલું આવર્તન દર્શાવે છે. તો ઉપરની માહિતી પરથી શું તારણ કાઢી શકાય?View Solution
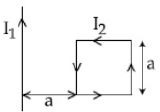
- 9આકૃતિમાં દર્શાવ્યા મુજબ $I_1$ પ્રવાહ પસાર થતાં લાંબા તારથી $a$ અંતરે $a$ બાજુવાળા ચોરસ લૂપમાથી $I_2$ પ્રવાહ પસાર થાય છે.તારને લીધે ચોરસ લૂપ પર લાગતું કુલ બળ કેટલું હશે?View Solution
- 10આપ્રશ્ન માં વિધાન $I$ અને વિધાન $II$ આપવામાં આવ્યા છે. યોગ્ય વિકલ્પ પસંદ કરો.View Solution
વિધાન $I$ : એમિટરની જેમ રેન્જ વધારે તેમ અવરોધ મોટો.
વિધાન $II$ : એમિટરની રેન્જ વધારવા માટે તેને સમાંતર વધારાનો શંટ જોડવો પડે.
