$R$ ત્રિજયા ધરાવતી બે પ્લેટને $d$ અંતરે મૂકતાં કેપેસિટન્સ $C$ બને છે.હવે $R/2$ ત્રિજયા ધરાવતો અને $d$ જાડાઇ ધરાવતો ડાઇઇલેકિટ્રક $6$ ને મૂકતાં નવું કેપેસિટન્સ કેટલુ થાય?
Diffcult
d
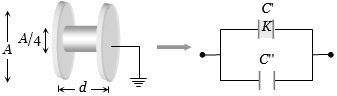
(d) Area of the given metallic plate \(A = \pi r^2\)
Area of the dielectric plate \(A' = \pi \,{\left( {\frac{r}{2}} \right)^2} = \frac{A}{4}\)
Uncovered area of the metallic plates
\( = A - \frac{A}{4} = \frac{{3A}}{4}\)
The given situation is equivalent to a parallel combination of two capacitor. One capacitor \((C')\) is filled with a dielectric medium \((K = 6)\) having area \(\frac{A}{4}\) while the other capacitor \((C'')\) is air filled having area \(\frac{{3A}}{4}\)
Hence
\( = \frac{{{\varepsilon _0}A}}{d}\left( {\frac{K}{4} + \frac{3}{4}} \right)\)\( = \frac{{{\varepsilon _0}A}}{d}\,\left( {\frac{6}{4} + \frac{3}{4}} \right) = \frac{9}{4}\,C\)
(d) Area of the given metallic plate \(A = \pi r^2\)
Area of the dielectric plate \(A' = \pi \,{\left( {\frac{r}{2}} \right)^2} = \frac{A}{4}\)
Uncovered area of the metallic plates
\( = A - \frac{A}{4} = \frac{{3A}}{4}\)
The given situation is equivalent to a parallel combination of two capacitor. One capacitor \((C')\) is filled with a dielectric medium \((K = 6)\) having area \(\frac{A}{4}\) while the other capacitor \((C'')\) is air filled having area \(\frac{{3A}}{4}\)
Hence
\( = \frac{{{\varepsilon _0}A}}{d}\left( {\frac{K}{4} + \frac{3}{4}} \right)\)\( = \frac{{{\varepsilon _0}A}}{d}\,\left( {\frac{6}{4} + \frac{3}{4}} \right) = \frac{9}{4}\,C\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
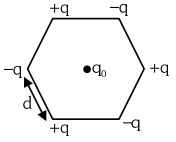
- 1છ વિદ્યુતભાર $+ q ,- q ,+ q ,- q ,+ q$ અને $- q$ ને આકૃતિમાં દર્શાવ્યા મુજબ $d$ બાજુના ષટ્કોણના શિરોબિંદુ પર મૂકેલા છે. અનંતથી ષટ્કોણના કેન્દ્રમાં $q _0$ વિદ્યુતભાર લાવવામાં માટે કેટલું કાર્ય કરવું પડે? $\left(\varepsilon_0-\right.$ મુક્ત અવકાશની પરમિટિવિટી)View Solution
- 2બે પ્લેટો વડે સમાંતર પ્લેટ કેપેસિટર રચેલ છે. દરેક પ્લેટનું ક્ષેત્રફળ $100\ cm^2, \,1\ mm$ અંતરે અલગ કરેલી છે. એક $5.0$ ડાઈ ઈલેકટ્રીક અચળાંંક ધરાવતા ડાઈ ઈલેકટ્રીક અને ડાઈ ઈલેકટ્રીક સ્ટ્રેન્થ $1.9 \times 10^7\ V/m$ પ્લેટોની વચ્ચે ભરવામાં આવે છે. ડાઈ ઈલેકટ્રીક બ્રેક ડાઉન કર્યા સિવાય કેપેસિટર પર સંગ્રહ કરી શકાતો મહત્તમ વિદ્યુતભાર શોધો.View Solution
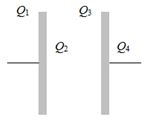
- 3$C$ કેપેસીટન્સ ધરાવતી આઇસોલેટેડ પ્લેટની ચાર સપાટી પરના વિદ્યુત ભારો $Q_1$, $Q_2$, $Q_3$, $Q_4$ આકૃતીમાં દર્શાવ્યા મુજબના છે. તો પ્લેટો વચ્ચેનો વિદ્યુત સ્થિતિમાનનો તફાવત....View Solution
- 4જો સમાંતર પ્લેટ સંધારકની પ્લેટ કે જેને બેટરી સાથે જોડવામાં આવેલ છે ને એકબીજાની નજીક ખસેડવામાં આવે છે ત્યારે. . . . . . . . .View Solution
$A$. તેમાં સંગ્રહિત વિધુતભાર વધે છે .
$B$. તેમાં સંગ્રહિત ઊર્જા ધટે છે.
$C$. તેની સંધારકતા વધે છે.
$D$. વિધુતભાર અને તેના સ્થિતિમાનનો ગુણોત્તર સમાન રહે છે.
$E$. વિધુત ભાર અને વોલ્ટેજનો ગુણાકાર વધે છે.
નીચ આપેલા વિકહ્પોમાંથી સૌથી યોગ્ય ઉતર પસંદ કરો.
- 5શૂન્યાવકાશમાં $3\, cm$ તથા $1\, cm$ ત્રિજ્યાવાળા ગોળાને એકબીજાથી $10\, cm$ અંતરે રાખેલ છે જો દરેક ગોળાઓને $10\, V$ જેટલો વિદ્યુતભારીત કરવામાં આવે તો તેમની વચ્ચેનું અપાકર્ષણ બળ....View Solution
- 6સમાંતર પ્લેટ કેપેસિટરની પ્લેટો વચ્ચેનું અંતર $0.05\, m$ છે. પ્લેટોની વચ્ચે $3 \times 10^4\,V/m$ મુલ્યનું વિ. ક્ષેત્ર સ્થાપિત કરવામાં આવે છે. તેને બેટરીથી દૂર કરી અને એક $0.01 \,m$ જાડાઈની ધાતુની અવિદ્યુતભારિત પ્લેટને (કેપેસિટર) દાખલ કરવામાં આવે છે. તો જો ધાતુની પ્લેટને બદલે $K = 2$ ડાઈ-ઈલેકટ્રીક અચળાંકની પ્લેટને મુકવામાં આવે તો સ્થિતિમાન તફાવત કેટલા.....$kV$ હશે ?View Solution
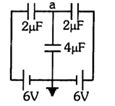
- 7આપેલા પરિપથ માટે, $2\ \mu F$ કેપેસિટર પરનો વોલ્ટેજ શોધો.View Solution
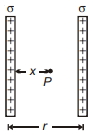
- 8બે અનંત લાંબી વિદ્યુતભારીત સમાન પૃષ્ઠો માટે, $P$ પાસે વિદ્યુતક્ષેત્ર કેટલું હશેView Solution
- 9$R_{1}$ અને $\mathrm{R}_{2}$ ત્રિજ્યા ધરાવતા બે વિદ્યુતભારિત ગોળાકાર સુવાહકોને એક તારથી જોડવામાં આવેલા છે. તો ગોળાઓની પૃષ્ઠ વિદ્યુતભાર ઘનતાઓનો ગુણોત્તર $\left(\sigma_{1} / \sigma_{2}\right)$ $.....$ છે.View Solution
- 10એક કણ $A$ અનો વિદ્યુતભાર $+q$ અને $B$ નો વિદ્યુતભાર $+9\ q$ છે. પ્રત્યેક કણનું દળ $m$ સમાન છે. જો બંને કણોને સ્થિર સ્થિતિએથી સમાન સ્થિતિમાન તફાવત સાથે છોડવામાં આવે તો તેઓની ઝડપનો ગુણોત્તર ....... હશે.View Solution
