કેપેસિટરના કિસ્સામાં \(E = (V/d)\), ધાતુની પ્લેટને દાખલ કર્યા પહેલા પ્લેટો વચ્ચેનો સ્થિતિમાન તફાવત
\(V = E \times d = 3 \times 10^4 \times 0.05 = 1.5\, kV\)
હવે ચાર્જિંગ બેટરીને દૂર કર્યા બાદ, કેપેસિટર એ અલગ કરેલું હોવાથી \(q\) = અચળ, જા \(C'\) અને \(V'\)
હવે પ્લેટને દાખલ કર્યા બાદ કેપેસિટન્સ અને સ્થિતિમાન હોય તો
\(q = CV = C'V'\,\,\,\,\,\,\,i.e.,\,\,V' = \frac{C}{{C\,'}}V\)
અને જેમ \({\text{C}} = \frac{{{\varepsilon _{\text{0}}}A}}{d}\,\,\) અને \({\text{C'}} = \frac{{{\varepsilon _{\text{0}}}A}}{{(d - t) + (t/K)}}\,\,\, \Rightarrow \,\,\,V' = \frac{{(d - t) + (t/K)}}{d} \times V\)
તેથી ધાતુની પ્લેટની બાબતમાં \({\text{K}} = \infty \,\,\,\,\)
\({V_M} = \left[ {\frac{{d - t}}{d}} \right] \times V = \left[ {\frac{{0.05 - 0.01}}{{0.05}}} \right] \times 1.5 = 1.2\,kV\)
અને જો ધાતુની પ્લેટને બદલે \(K = 2\) ડાઈ-ઈલેકટ્રીક સાથે દાખલ કરેલ હોય તો
\({V_D} = \left[ {\frac{{(0.05 - 0.01) + (0001/2)}}{{0.05}}} \right] \times 1.5 = 1.35\,kV\)
Download our appand get started for free
Similar Questions
- 1કણ $A$ પરનો વિદ્યુતભાર $+q$ તથા કણ $B$ પરનો વિદ્યુતભાર $+4q$ છે તથા તેમના દળ સમાન છે જ્યારે તેમની સમાન વિદ્યુત સ્થીતીમાનના તફાવત હેઠળ સ્થીર સ્થીતીમાંથી મુક્ત કરવામાં આવે તો તેમની ઝડપ $V_A / V_B$ નો ગુણોત્તર....View Solution
- 2જ્યારે સમાંતર પ્લેટ કેપેસીટરની બે પ્લેટો વચ્ચેનું અંતર $6\, cm$ હોય ત્યારે તેનું કેપેસીટન્સ $15\ \mu F$ છે પ્લેટો વચ્ચેનું અંતર $2\ cm$ સુધી ઘટાડવામાં આવે તો સમાંતર પ્લેટ કેપેસીટરનું કેપેસીટન્સ....$\mu F$View Solution
- 3ગોળીય કવચ કેપેસિટરની બહારની ત્રિજયા $R$ છે.બહારની અને અંદરની ત્રિજયાનો તફાવત $x$ છે.તો તેનું કેપેસિટન્સ કોના સપ્રમાણમાં હોય?View Solution
- 4એક સમાંતર પ્લેટ કેપેસિટર પાસે $20 \,kV$ સ્થિતિમાન અને $2 \times 10^{-4} \,\mu F$ કેપેસિટન્સ છે. જો પ્લેટનું ક્ષેત્રફળ $0.01\,m^2$ હોય અને પ્લેટો વચ્ચેનું અંતર $2\,mm$ હોય તો ઉર્જા શોધો.View Solution
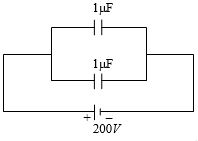
- 5આપેલ તંત્રની કુલ ઊર્જા કેટલા........$joules$ થાય?View Solution
- 6$R$ અને $4 R$ ત્રિજયાના સમકેન્દ્રિય ધાત્વિય ગોળીય કવચ પર અનુક્રમે $Q _{1}$ અને $Q _{2}$ વિજભાર છે. બંને સમકેન્દ્રિય ધાત્વિય ગોળીય કવચની પૃષ્ઠ વિજભાર ઘનતા સમાન હોય તો તેમના વિદ્યુતસ્થિતિમાનનો તફાવત $V ( R )- V (4 R )$ કેટલો હશે?View Solution
- 7$5\ \mu C$ અને $10\ \mu C$ ના બે વિદ્યુતભારો એકબીજાથી $1\ m$ દૂર રહેલા ચે, તેમને હવે એકબીજાથી $0.5\ m$ અંતરે લાવવા કરવું પડતું કાર્ય ...... છે.View Solution
- 8એક $8\; mC$ વિધુતભાર ઉગમબિંદુએ રહેલો છે. એક નાના $-2 \times 10^{-9} \;C$ વિધુતભારને $P (0,0,3\; cm )$ બિંદુથી $R (0,6\; cm , g \;cm )$ બિંદુએ થઈ $Q (0,4\; cm , 0),$ બિંદુએ લાવવા માટે કરેલું કાર્ય શોધો..View Solution
- 9$-10$ વોલ્ટ જેટલું સ્ચિતિમાન ધરાવતાં એક બિંદુ $V$ જેટલું સ્થિતિમાન ધરાવતાં એક બિંદુ પર $2C$ જેટલો ચાર્જને લાવવા માટે $50$ જુલ જેટલું કાર્ય કરવું પડતું હોય તો $V$ નું મુલ્ય $....$View Solution
- 10$R$ ત્રિજ્યાની એક પાતળી સુવાહક કવચ પરનો વિદ્યુતભાર $q$ છે. બીજો $Q$ વિદ્યુતભાર કવચના કેન્દ્ર આગળ મૂકેલો છે. કવચના કેન્દ્રથી $R/2$ અંતરે $P$ બિંદુ આગળ વિદ્યુત શાસ્ત્રનું વિદ્યુત સ્થિતિમાન ........ છે.View Solution
