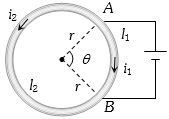
$R$ ત્રિજયા ધરાવતી રીંગ પરના $A$ અને $B$ બિંદુ વચ્ચે બેટરી લગાવેલ છે. $AB$ એ કેન્દ્ર આગળ $ \theta $ ખૂણો બનાવે છે.તો કેન્દ્ર પર ચુંબકીયક્ષેત્ર...
IIT 1995, Medium
d
(d) Directions of currents in two parts are different, so directions of magnetic fields due to these currents are opposite. Also applying Ohm’s law across \(AB\)
\({i_1}{R_1} = {i_2}{R_2} \Rightarrow {i_1}{l_2} = {i_2}{l_2}\) \(\left( {\;R = \rho \frac{l}{A}} \right)\)
Also \({B_1} = \frac{{{\mu _o}}}{{4\pi }} \times \frac{{{i_1}{l_1}}}{{{r^2}}}\) and \({B_2} = \frac{{{\mu _o}}}{{4\pi }} \times \frac{{{i_2}{l_2}}}{{{r^2}}}\) (\(\;l = r\theta \))
\(\therefore \,\frac{{{B_2}}}{{{B_1}}} = \frac{{{i_1}{l_1}}}{{{i_2}{l_2}}} = 1\)
Hence, two field induction’s are equal but of opposite direction. So, resultant magnetic induction at the centre is zero and is independent of \(\theta \).
(d) Directions of currents in two parts are different, so directions of magnetic fields due to these currents are opposite. Also applying Ohm’s law across \(AB\)
\({i_1}{R_1} = {i_2}{R_2} \Rightarrow {i_1}{l_2} = {i_2}{l_2}\) \(\left( {\;R = \rho \frac{l}{A}} \right)\)
Also \({B_1} = \frac{{{\mu _o}}}{{4\pi }} \times \frac{{{i_1}{l_1}}}{{{r^2}}}\) and \({B_2} = \frac{{{\mu _o}}}{{4\pi }} \times \frac{{{i_2}{l_2}}}{{{r^2}}}\) (\(\;l = r\theta \))
\(\therefore \,\frac{{{B_2}}}{{{B_1}}} = \frac{{{i_1}{l_1}}}{{{i_2}{l_2}}} = 1\)
Hence, two field induction’s are equal but of opposite direction. So, resultant magnetic induction at the centre is zero and is independent of \(\theta \).

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2 \mathrm{~m}$ લંબાઈ ની બાજુ અને $2 \mathrm{~A}$ પ્રવાહ ધરાવતા એક ચોરસ ગાળાને તેની બાજુઓ $x-y$ અક્ષને સમાંતર રહે તે રીતે મૂકેલ છે. ક્ષેત્ર $x-1$ સમતલમાંથી ચુંબકીય પસાર થાય છે અને તે $\vec{B}=B_0(1+4 x) \hat{\mathrm{k}}$, જ્યાં $B_0=5$ ટેસલા વડે રજૂ થાય છે. ગાળા દ્વારા અનુભવાતું પરિણ઼ામી ચુંબકીય બળ ............... $\mathrm{N}$ છે.View Solution
- 2એક લાંબી, સુરેખ અને પાતળી દિવાલવાળી પાઇપમાંથી વિદ્યુતપ્રવાહ $I$ વહે છે. તો નીચેનામાંથી ક્યું વિધાન સાયું છે?View Solution
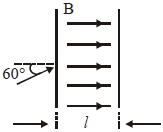
- 3$l$ લંબાઈ માં $0.3\,T$ નું ચુંબકીય ક્ષેત્ર છે. પ્રોટોન આ ક્ષેત્ર સાથે $60$ ના ખૂણે $4 \times 10^{5}\, ms ^{-1}$ ના વેગ થી દાખલ થાય છે. $10$ પરિણામમાં પ્રોટોન $l$ અંતર કાપતો હોય તો $l= ....... m$View Solution
(પ્રોટોનનું દળ $=1.67 \times 10^{-27} \,kg,$ પ્રોટોનનું વિધુતભાર $\left.=1.6 \times 10^{-19}\, C \right)$
- 4$100\,V$ ના વિદ્યુતસ્થિતિમાનના તફાવત થી પ્રવેગિત કરેલ $2\,\mu\,C$ નો વિદ્યુતભાર $4\,mT$ તીવ્રતાના સમાન ચુંબકીયક્ષેત્રમાં ક્ષેત્રને લંબ દિશામાં દાખલ થાય છે. વિદ્યુતભારીત કણ ચુંબકીય ક્ષેત્રની અંદર $3\,cm$ ત્રિજ્યાનું અર્ધવર્તુળ પૂર્ણ કરે છે. વિદ્યુતભારીત કણનું દળ $........\times 10^{-18}\,kg$ હશે.View Solution
- 5પૃથ્વીની સપાટીથી $4$ $ m$ ઊંચાઇએ એક સુરેખ વાહક તાર સમક્ષિતિજ દિશામાં પૂર્વ-પશ્ચિમ રાખેલ છે.તેમાંથી $100$ $A$ જેટલો વિદ્યુતપ્રવાહ પૂર્વ થી પશ્ચિમ તરફ વહે છે.આ તારની બરાબર નીચે પૃથ્વીની સપાટી પર ઉદ્ભવતું ચુંબકીયક્ષેત્ર ______ હશે.View Solution
${\mu _o}$$=4$$\pi $$ \times 10^{-7}$ $\frac{{Tm}}{A}$ લો. પૃથ્વીનું ચુંબકીયક્ષેત્ર અવગણો.
- 6$R$ ત્રિજયાની પ્રવાહધારિત રીંગની અક્ષ પર કેટલા અંતરે ચુંબકીયક્ષેત્ર કેન્દ્ર પરના ચુંબકીયક્ષેત્ર કરતાં $ \frac{1}{8} $માં ભાગનું થાય?View Solution
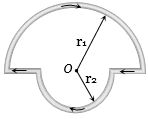
- 7આપેલ પરિપથમાં કેન્દ્ર $O$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 8$m$ દળ અને $Q$ વિદ્યુતભારનો વિદ્યુતભરીત કણ $r$ ત્રિજ્યાના વર્તુળાકાર પથ પર ચુંબકીય ક્ષેત્ર $B$ને લંબ ગતિ કરે છે તો તેનો આવર્તકાળ કેટલો થાય?View Solution
- 9$G$ જેટલો અવરોધ અને $S$ જેટલો શંટ જોડી રૂપાંતરીત કરેલા ગેલ્વેનોમીટરમાં વાસ્તવમાં થતા કોણાવર્તનો $n$ છે. જ્યારે તેનો ગુણવત્તા અંક (figure of merit) $K$ હોય તો કુલ પ્રવાહ $I$....... થશે.View Solution
- 10View Solutionજો સમાન વેગમાન ધરાવતો ઇલેક્ટ્રોન અને પ્રોટોન ચુંબકીયક્ષેત્રને લંબ પ્રવેશે, તો ...
