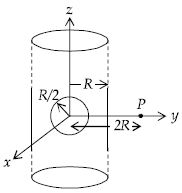
$R$ ત્રિજ્યા ધરાવતો અનંત ધન નળાકારમાં અચળ વિજભાર કદ ઘનતા $\rho$ છે. તેના અંદર $R/2$ ત્રિજ્યા ધરાવતી ગોળીય બખોલ છે. જેનું કેન્દ્ર અક્ષ પર છે. નળાકારની અક્ષથી $2R$ અંતરે આવેલ $P$ બિંદુએ વિદ્યુતક્ષેત્ર $\frac{{23\rho R}}{{16K{\varepsilon _0}}}$ હોય તો $K$ નું મૂલ્ય કેટલું હશે?

Diffcult
a
We suppose that the cavity is filled up by a positive as well as negative volume charge of \(\rho .\) So the electric field now produced at \(P\) is the superposition of two electric fields.
We suppose that the cavity is filled up by a positive as well as negative volume charge of \(\rho .\) So the electric field now produced at \(P\) is the superposition of two electric fields.
\((i)\) The electric field created due to the infinitely long solid cylinder is
\(E_{1}=\frac{\rho R}{4 \varepsilon_{0}}\) directed towards the \(+Y\) direction
\((ii)\) The electric field created due to the spherical negative charge density
\(\mathrm{E}_{2}=\frac{\rho \mathrm{R}}{96 \varepsilon_{0}}\) directed towards the \(-Y\) direction.
\(\therefore \) The net electric field is
\(\mathrm{E}=\mathrm{E}_{1}-\mathrm{E}_{2}=\frac{1}{6}\left[\frac{23 \rho \mathrm{R}}{16 \varepsilon_{0}}\right]\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\overrightarrow{ p }$ ડાઈપોલ મોમેન્ટ ધરાવતા ડાઈપોલના કેન્દ્રથી $r$ અંતરે વિષુવવૃતીય સમતલ પર રહેલા બિંદુ આગળ વિધુતક્ષેત્ર ........... મળે ($r >>$ ડાઈપોલના બે વિધુતભાર વચ્ચેનું અંતર,$\varepsilon_{0}$ મુક્ત અવકાશની પરમિટિવિટી)View Solution
- 2$T$ આવર્તકાળ ધરાવતા લોલક રહેલ લોખંડનો ગોળો ઋણ વિજભાર ધરાવે છે.જો તેને એક ધન વિજભારિત ધાતુની પ્લેટ પર દોલનો કરાવવામાં આવે તો આવર્તકાળ.....View Solution
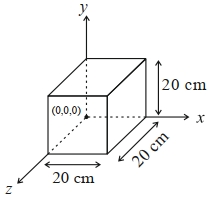
- 3વિદ્યુતક્ષેત્રને $\vec{E}=4000 x^2 \hat{i} \frac{ V }{ M }$ સમીકરણ વડે રજૂ કરેલ છે. $20\,cm$ ની બાજુ (આકૃત્તિમાં દર્શાવ્યા અનુસાર) ધરાવતા સમધનમાંથી પસાર થતું ફ્લક્સ $................V\,cm$ થશે.View Solution
- 4દરેક $+q$ જેટલો વિદ્યાતભાર ધરાવતા બે નાના ગોળાઓ એક $2a$ લંબાઈની અવાહક દોરીથી જોડેલા છે તો દોરીમાં તણાવબળ કેટલું હશે?View Solution
- 5સમાન વિરૂદ્ધ નિશાની ધરાવતી પૃષ્ઠ વિદ્યુતભાર ઘનતા ($\sigma$ $= 26.4 \times 10^{-12} \ C/m^2$) વાળી બે સમાંતર વિશાળ પાતળી ધાતુની તકતી છે. આ તકતી વચ્ચેનું વિદ્યુતક્ષેત્ર ........$N/C$ છે.View Solution
- 6સમાન વિદ્યુતભાર ધરાવતા બે સમાન ગોળાઓને એક આધારબિંદુથી સરખી લંબાઈની દોરી વડે લટકાવેલ છે. ત્યારે બે દોરી વચ્ચેનો કોણ $30^o$ છે. જ્યારે $0.8\, g\, cm^{-3}$ ઘનતાના પ્રવાહીમાં ડૂબાડવામાં આવે ત્યારે બે દોરી વચ્ચેનો કોણ ગોળાઓ હવામાં હતા તયારે જેટલો હતો તેટલો જ રહે છે. જો ગોળાઓના દ્રવ્યની ઘનતા $1.6 \,g \,cm^{-3}$ હોય તો પ્રવાહીનો ડાઈઈલેક્ટ્રિક અચળાંક ........ છે.View Solution
- 7View Solutionવિદ્યુત ડાઈપોલની વિષુવ રેખા પરના એક બિંદુ માટે વિદ્યુતક્ષેત્રની તીવ્રતાની દિશા ....... છે.
- 8$1\ gm$ દળના ઘન ગોળામાં $5 \times 10^{21}$ પરમાણુ છે, $0.01\%$ પરમાણુ દીઠ એક ઇલેકટ્રોન દૂર કરતાં ગોળો કેટલા .....$C$ વિદ્યુતભાર પ્રાપ્ત કરે?View Solution
- 9ડાયપોલના કેન્દ્રથી $r$ અંતરે અક્ષ પર વિદ્યુતક્ષેત્ર $E$ છે.હવે જો ડાયપોલને $90°$ ફેરવવામાં આવે,તો તે બિંદુએ વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 10$ + \sigma $ અને $ - \sigma $ પૃષ્ઠ વિધુતભાર ઘનતા ધરાવતા અનંત લંબાઈના સમતલને સૂક્ષ્મ અંતરે સમાંતર મૂકેલા છે બંને પ્લેટ વચ્ચે શૂન્યઅવકાશ છે જો ${\varepsilon _0}$ એ શૂન્યાવકાશની પરમિટિવિટી હોય તો બે પ્લેટ વચ્ચેના અવકાશમાં વિધુતક્ષેત્ર .............. મળેView Solution
