From figure, \(\mathrm{d} \ell=\mathrm{Rd} \theta\)
Charge on \(d \ell=\lambda \mathrm{Rd} \theta\)
where \(\lambda=\) linear charge density.
Electric field at centre due to \(d \ell\)
\(\mathrm{dE}=\mathrm{k} \cdot \frac{\lambda \mathrm{Rd} \theta}{\mathrm{R}^{2}}\)
We need to consider only the component \(dE\) \(\cos \theta,\) as the component \(dE\) sin \(\theta\) will cancel out.
\(\therefore \) Total field at centre \(=2 \int_{0}^{\pi / 2} \mathrm{dE}\, \cos \theta\)
\(=2 \int_{0}^{\pi / 2} \frac{\mathrm{k} \lambda \mathrm{R}\, \cos \theta}{\mathrm{R}^{2}} \mathrm{d} \theta=\frac{2 \mathrm{k} \lambda}{\mathrm{R}} \int_{0}^{\pi / 2} \cos\, \theta \mathrm{d} \theta\)
\(=\frac{9}{2 \pi^{2} \epsilon_{0} R^{2}} \quad\left(\text { since } \lambda=\frac{q}{\pi R}\right)\)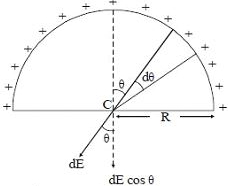
Download our appand get started for free
Similar Questions
- 1$1\, g$ જેટલા સમાન દળના બે સમાન ગોળાઓ પરનો સમાન વિદ્યુતભાર $10^{-9}\, C$ છે. જેમને સમાન લંબાઈની દોરીઓ વડે મુક્ત કરવામાં આવે છે. જો ગોળાનો કેન્દ્રો વચ્ચેનું અંતર $0.3\, cm$ હોય તો દોરીના પ્રક્ષેપણ કોણ શિરોલંબ ઘટક સાથે ...... હશે.View Solution
- 2બે સમાન ગોળાઓ $A$ અને $B$ને જ્યારે હવામાં ચોક્કસ અંતરે રાખવામાં આવે છે ત્યારે તે $F$ જેટલાં બળથી એકબીજાને અપાકર્ષે છે. ત્રીજો સમાન અવિદ્યુતભારીત ગોળો $C$ પ્રથમ ગોળા $A$ના અને ત્યારબાદ ગોળા $B$ના સંપર્કમાં લાવવામાં આવે છે. છેલ્લે તેને ગોળાઓ $A$ અને $B$ ના મધ્યબિંદુ પર મૂકવામાં આવે છે. ગોળા $C$ પર લાગતું બળ $...........$ હશે.View Solution
- 3ડાયપોલની અક્ષ પર વિદ્યુતક્ષેત્ર ${E_a}$ અને ડાયપોલની વિષૃવવૃત રેખા પર વિદ્યુતક્ષેત્ર ${E_e}$ છે.જો આ બંને બિંદુઓ સમાન અંતરે હોય,તો...View Solution
- 4આકૃતિમાં અનિયમિત વિધુતક્ષેત્ર $x-$ અક્ષની દિશામાં છે વિધુતક્ષેત્ર ધન $x-$ અક્ષ પર નિયમિત દરથી વધે છે વિધુતડાઈપોલને વિધુતક્ષેત્રમાં મૂકવામાં આવે છે તો નીચનામાંથી ક્યુ વિધાન સાચું થાય ?View Solution
- 5અનંત ધનરેખીય વિદ્યુતભાર ફરતે $0.1 \,m$ ત્રિજ્યાના વર્તુંળમાં એક ઇલેક્ટ્રોન ભ્રમણ કરે છે. જો રેખીય વિદ્યુતભાર ઘનતા $1\,\mu C / m$, હોય, તો ઈલેક્ટોનનો વેગ $m / s$ માં ............. $\times 10^7$ છે.View Solution
- 6View Solutionએક ધન વિદ્યુતભારીત લોલક ઉપર તરફના એકરૂપ વિદ્યુતક્ષેત્રમાં દોલન કરે છે. તેનો આવર્તકાળ જ્યારે તે વિદ્યુતક્ષેત્ર વગર દોલન કરે તેની સરખામણીમાં
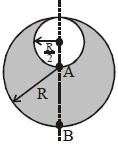
- 7$\mathrm{R}$ ત્રિજ્યા ધરાવતા ગોળા પર વિજભારઘનતા $\rho$ છે.જો તેમાથી $\frac{\mathrm{R}}{2}$ ત્રિજ્યા ધરાવતો ભાગ કાપી નાખવામાં આવે તો $\frac{\left|\overrightarrow{\mathrm{E}}_{\mathrm{A}}\right|}{\left|\overrightarrow{\mathrm{E}}_{\mathrm{B}}\right|}$ નો ગુણોત્તર કેટલો થાય? જ્યાં $\overrightarrow{\mathrm{E}}_{\mathrm{A}}$ અને $\overrightarrow{\mathrm{E}}_{\mathrm{B}}$ બિંદુ $\mathrm{A}$ અને બિંદુ $\mathrm{B}$ પાસે વિદ્યુતક્ષેત્ર છે.View Solution
- 8$20\, \mu {C}$ અને $-5\, \mu {C}$ બે વિદ્યુતભાર ધરાવતા બે કણો ${A}$ અને ${B}$ વચ્ચેનું અંતર $5\, {cm}$ છે. ત્રીજા વિદ્યુતભારને કેટલા અંતરે મૂકવાથી તેના પર લાગતું વિદ્યુતક્ષેત્ર શૂન્ય થાય?View Solution
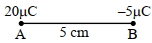
- 9ડ્યુટ્રોન અને $\alpha$ - કણ હવામાં એકબીજાથી $1\,\mathop A\limits^o $ અંતરે આવેલા છે. ડ્યુટ્રોનને લીધે $\alpha$ - કણ પર લાગતા વિદ્યુતક્ષેત્રનું મૂલ્ય ........ હશે.View Solution
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે બે આદર્શ ડાયપોલ $A$ અને $B$ જેની ડાયપોલ મોમેન્ટ અનુક્રમે $p_{1}$ અને $p_{2}$ છે, તેને સમતલમાં તેના કેન્દ્ર $O$ પર રહે તેમ મુકેલ છે. ડાયપોલ $A$ ની અક્ષ પરના બિંદુ $C$ પર, પરિણામી વિદ્યુતક્ષેત્ર અક્ષ સાથે $37^{\circ}$ ની ખૂણો બનાવે છે. $A$ અને $B$ ની ડાયપોલ મોમેન્ટ નો ગુણોત્તર, $\frac{P_{1}}{P_{2}}$ કેટલો થાય?View Solution
($\sin 37^{\circ}=\frac{3}{5}$ લો)