રાસાયણિક પ્રક્રિયા નીચે આપેલ તબક્કામાંથી પસાર થાય છે.
તબક્કો $: I :$ $2A $ $\rightleftharpoons$ $ X $ ઝડપી.
તબક્કો $II :$ $X + B $ $\rightleftharpoons$ $Y$ ધીમી
તબક્કો $III :$ $Y + B$ નીપજ ઝડપી આખી પ્રક્રિયા કયા નિયમ પર આધારિત છે ?
Medium
Download our app for free and get started
d
ધીમો તબક્કો $x/dt = K' [x] [B]$
ધીમો તબક્કો $x/dt = K' [x] [B]$
પ્રથમ તબક્કા માટે વેગ $= [x] = K_1 [A]$
બીજા તબક્કા માટે વેગ $= K_2 [X] [B] = K_2 (K_1[A]^2)[B] $
( $\because $ સમીકરણ $ (1) $ પરથી) $=K[A]^2[B] $ જ્યાં $K = K_1 . K_2$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આપેલ રાસાયણિક પ્રક્રિયા માટે,View Solution
$\gamma_{1} A +\gamma_{2} B \rightarrow \gamma_{3} C +\gamma_{4} D$
જ્યાં $v_{1}, v_{2}, v_{3}$ અને $v_{4}$ એ પૂર્ણાંક છે. $(i.e.$ $\left.1,2,3,4 \ldots . .\right)$
$10$ સેકન્ડોના અંતરાલ માં $C$ ની સાંદ્રતા $10\,m\,mol\,dm ^{-3}$ માંથી $20\,m\,mol\,dm ^{-3}$ માં ફેરફાર થાય છે.$D$નો દશ્ય થવાનો વેગ એ $B$ના અદશ્ય થવાના વેગ કરતા $1.5$ ગણો છે, ને $A$ ના અદશ્ય થવાના વેગ કરતા બમણો છે.પ્રાયોગિક રીતે $D$ના દશ્ય થવાનો વેગ $9,m\,mol\,dm ^{-3} \,s ^{-1}$ શોધવામાં આવ્યો.તેથી પ્રક્રિયાનો વેગ $\dots\dots\,\,m\,mol$$dm ^{-3} s ^{-1}.$
- 2$25\,^oC$ એ દર અચળાંક, સક્રિયકરણ ઊર્જા અને રાસાયણિક પ્રક્રિયાનાં આર્હેંનિયસ પરિબળો અનુક્રમે $3.0\times 10^{-4} \,s^{-1}, 104.4 \,kJ$ મોલ$^{-1} $ અને $6.0 \times 10^{14}\, s^{-1}$ છે. તો $T\rightarrow \infty$ તરીકે દર અચળાંકનું મૂલ્ય શોધો.View Solution
- 3View Solutionદ્વિતીય ક્રમની પ્રક્રિયા માટે વેગ-અચળાંકનો એકમ ......
- 4નીચે આપેલા કોષ્ટકમાં આપેલ પરિણામો નીચેની પ્રક્રિયાના ગતિ અભ્યાસ દરમિયાન પ્રાપ્ત થયા:View Solution
$2 A + B \longrightarrow C + D$
પ્રયોગ $[ A ] / molL ^{-1}$ $[ B ] / molL ^{-1}$ પ્રાથમિક $rate/molL$ $^{-1}$ $\min ^{-1}$ $I$ $0.1$ $0.1$ $6.00 \times 10^{-3}$ $II$ $0.1$ $0.2$ $2.40 \times 10^{-2}$ $III$ $0.2$ $0.1$ $1.20 \times 10^{-2}$ $IV$ $X$ $0.2$ $7.20 \times 10^{-2}$ $V$ $0.3$ $Y$ $2.88 \times 10^{-1}$ આપેલા ટેબલ માં $X$ અને $Y$ અનુક્રમે શું હશે ?
- 5$A$ $\rightarrow$ $ B$ આઈસોમરાઈઝેશન પ્રથમ પ્રક્રિયા માટેનો દર અચળાંક $ 4.5 \times 10^{-3}$ છે. જો $A$ ની પ્રારંભિક સાંદ્રતા $1\,M$ હોય, તો $1$ કલાક પછી પ્રક્રિયાનો દર શોધો?View Solution
- 6અચળ તાપમાન પ૨ વાયુ અવસ્થામાં નીચે આપેલ એક તબક્કીય પ્રક્રિયા ને ધ્યાનમાં લો.View Solution
$2 \mathrm{~A}_{(\mathrm{g})}+\mathrm{B}_{(\mathrm{g})} \rightarrow \mathrm{C}_{(\mathrm{g})}$
જ્યારે પ્રક્રિયા, $A$ નું $1.5 \mathrm{~atm}$ દબાણ અને $\mathrm{B}$ નાં $0.7 \mathrm{~atm}$ દબાણ સાથે પ્રારંભ (શરૂ) કરવામાં આવ્યો હોય ત્યારે પ્રક્રિયાનો પ્રારંભિક વેગ $r_1$ તરીક નોંધવામાં આવ્યો. થોડાક સમય પછી, જ્યારે $C$ નું દબાણ $0.5 \mathrm{~atm}$ થાય છે ત્યારે $r_2$ વેગ નોંધવામા આવ્યો, $r_1: r_2$ ગુણોત્તર ............ $\times 10^{-1}$ છે.
(નજીક નો પૂર્ણાક)
- 7પ્રકિયા $A \to B$ માટે ${K_1} = {10^8}\,{e^{ - 6000/8.34\,\,T}}$ અનેView Solution
પ્રક્રિયા $P \to Q$ માટે ${K_2} = {10^{10}}\,{e^{ - 8000/8.34\,\,T}}$ હોય તો ....... $K$ તાપમાને $K_1 = K_2$ થશે.
- 8જો પ્રક્રિયક $ B$ ની સાંદ્રતા બમણી થાય તો પ્રક્રિયક $A$ અને $B$ વચ્ચેની પ્રક્રિયાનો દર પ્રારંભિક દર $1/4$ જેટલો થાય છે. પ્રક્રિયક $B$ ના સંદર્ભમાં પ્રક્રિયાનો ક્રમ ...... થશે.View Solution
- 9શૂન્ય ક્રમ પ્રક્રિયાનો દર અચળાંક $0.2 $ મોલ $m^{-3}\,h^{-1}$ છે. જો પ્રક્રિયકની સાંદ્રતા $30$ મિનિટ પછી $0.05 $ મોલ $m^{-3}$ હોય તો તેની પ્રારંભિક સાંદ્રતા ....... મોલ $ m^{-3}$ થશે.View Solution
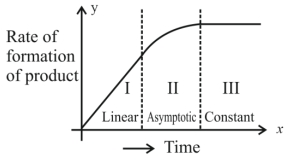
- 10એક નિશ્ચિત રાસાયણિક પ્રક્રિયા $X \rightarrow Y$ માટે, નીપજના બનવાનો દર વિરુદ્ધ સમયનો ગ્રાફ (આલેખ) એ આકૃતિમાં દર્શાવેલ છે. નીચે આપેલામાંથી સાચાં વિધાન/નોની સંખ્યા $..............$ છે.View Solution
$(A)$ સમગ્ર પ્રક્રિયાનો ક્રમ છે.
$(B)$ આ પ્રક્રિયાનો ક્રમ શોધી શકાતો નથી.
$(C)$ $I$ અને $III$ વિભાગ માં, પ્રક્રિયા અનુક્રમે પ્રથમ અને શૂન્ય ક્રમની છે.
$(D)$ વિભાગ $II$ માં, પ્રક્રિયા પ્રથમક્રમની છે.
$(E)$ વિભાગ $II$ માં, પ્રક્રિયાનો ક્રમ $0.1$ થી $0.9$ વિસ્તાર માં છે.
