\({\frac{M g}{A}=P_{0}}\) \( {P_{0} V_{0}^{\gamma}=P V^{\gamma}}\)
\({\mathrm{Mg}=\mathrm{P}_{0} \mathrm{A}}{\ldots(1)}\) \( {P_{0} A x_{0}^{\gamma}=P A\left(x_{0}-x\right)^{\gamma}}\)
\(P=\frac{P_{0} x_{0}^{\gamma}}{\left(x_{0}-x\right)^{\gamma}}\)
Let piston is displaced by distance \(x\)
\(M g-\left(\frac{P_{0} x_{0}^{\gamma}}{\left(x_{0}-x\right)^{\gamma}}\right) A=F_{\text {restoring }}\)
\(P_{0} A\left(1-\frac{x_{0}^{\gamma}}{\left(x_{0}-x\right)^{\gamma}}\right)=F_{\text {restoring }} \quad\left[x_{0}-x \approx x_{0}\right]\)
\(F=-\frac{\gamma P_{0} A x}{x_{0}}\)
Frequency with which piston executes \(SHM.\)
\(f=\frac{1}{2 \pi} \sqrt{\frac{\gamma P_{0} A}{x_{0} M}}=\frac{1}{2 \pi} \sqrt{\frac{\gamma P_{0} A^{2}}{M V_{0}}}\)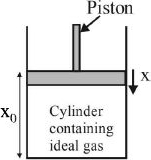
Download our appand get started for free
Similar Questions
- 1એક સાદા લોલક માટે,ગતિઊર્જા $(KE)$ અને સ્થિતિઊર્જા $(PE)$ વિરુદ્વ સ્થાનાંતર $d$ નો આલેખ દોરેલ છે. નીચે આપેલ પૈકી કયો આલેખ તેમને સાચી રીત દર્શાવે છે. ( આલેખો ફકત રેખાકૃતિ સૂચવે છે અને તેઓ એક જ સ્કેલ પર દોરેલ નથી? )View Solution
- 2$M$ દળ અને $R$ જેટલી ત્રિજ્યા ધરાવતી તક્તી તેના પરિઘ પરના કોઈ બિંદુ બાંધીને લટકાવેલ છે. જે ઊર્ધ્વ દિશામાં લટકાવેલ છે. તેના દોલનોનો આવર્તકાળ કેટલો થશે ?View Solution
- 3સરળ આવર્ત ગતિ કરતા કણનો વેગ સ્થાનાંતર $(x)$ સાથે $4 v^2=50-x^2$ અનુસાર બદલાય છે. દોલનોનો આવર્તકાળ $\frac{x}{7}$ છે. તો $x$ નું મૂલ્ય $............$ છે.View Solution
- 4$y = 2\, (cm)\, sin\,\left[ {\frac{{\pi t}}{2} + \phi } \right]$ સરળ આવર્તગતિમાં પ્રવેગનું મહત્તમ મૂલ્ય કેટલું થાય?View Solution
- 5કણ $X-$ અક્ષ પર સરળ આવર્તગતિ કરે છે, તો તેના પર લાગતું બળ શેના વડે આપી શકાય?View Solution
જ્યાં $A$ અને $K$ ધન અચળાંકો છે.
- 6સેકન્ડ લોલકનો આવર્તકાળ $2\, sec$ છે. તેના પોલા ગોળાનું દળ $50\ gram$ છે. તેને સમાન ત્રિજ્યાવાળા અને $100\; gram$ દળ ધરાવતા ઘન ગોળા વડે બદલવામાં આવે છે. તો તેનો નવો આવર્તકાળ ..... $\sec$ થશે.View Solution
- 7View Solutionસરળ આવર્ત ગતિ કરતાં કણની કુલ ઉર્જા કોના સમપ્રમાણમાં હોય?
- 8સરળ આવર્ત ગતિ કરતાં પદાર્થનું સરળ આવર્ત ગતિનું સમીકરણ $ x(t) = a\cos (\omega t + \theta ) $ છે,શરૂઆતની સ્થિતિ $1\,cm$ અને શરૂઆતનો વેગ $ \pi \,cm/s $ છે,જો કોણીય આવૃતિ $ \pi \,rad/s $ હોય,તો કંપવિસ્તાર કેટલો થાય?View Solution
- 9$l$ લંબાઈના સાદા લોલકને સમતોલન સ્થાનથી શિરોલંબ સાથે $\theta$ ખૂણે સ્થાનાંતર કરવવામાં આવે છે. જો તેને મુક્ત કરવામાં આવે તો લોલકના સૌથી નીચેના સ્થાને તેનો વેગ કેટલો થાય?View Solution
- 10સ્પ્રિંગ જેની મૂળભૂત લંબાઈ $\ell $ અને બળ અચળાંક $k$ છે તેને $\ell_1$ અને $\ell_2$ લંબાઈના બે ભાગમાં વિભાજિત કરવામાં આવે છે જ્યાં $\ell_1 = n\ell_2$ અને $n$ પૂર્ણાક છે, તો બંને સ્પ્રિંગના બળ અચળાંકનો ગુણોત્તર $k_1/k_2$ =View Solution
