$l$ લંબાઈના સાદા લોલકને સમતોલન સ્થાનથી શિરોલંબ સાથે $\theta$ ખૂણે સ્થાનાંતર કરવવામાં આવે છે. જો તેને મુક્ત કરવામાં આવે તો લોલકના સૌથી નીચેના સ્થાને તેનો વેગ કેટલો થાય?
AIPMT 2000, Medium
c
(c) If suppose bob rises up to a height h as shown then after releasing potential energy at extreme position becomes kinetic energy of mean position
(c) If suppose bob rises up to a height h as shown then after releasing potential energy at extreme position becomes kinetic energy of mean position
\( \Rightarrow mgh = \frac{1}{2}mv_{\max }^2\)
\( \Rightarrow {v_{\max }} = \sqrt {2gh} \)
Also, from figure \(\cos \theta = \frac{{l - h}}{l}\)
\( \Rightarrow h = l(1 - \cos \theta )\)
So, \({v_{\max }} = \sqrt {2gl(1 - \cos \theta )} \)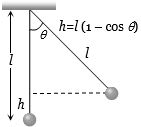
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$T$ આવર્તકાળ સાથે એક કણ સરળ આવર્ત ગતિ કરે છે. જો તેની કુલ યાંત્રિક ઉર્જાનો આવર્તકાળ $T^{\prime}$ હોય તો $\frac{T^{\prime}}{T}$ તો કેટલો થશે?View Solution
- 2View Solutionપાણી ભરેલા પોલા ગોળાને દોરી વડે લટકાવેલ છે.પાણી તળીયામાં રહેલા છિદ્ર દ્રારા બહાર આવે તો સરળ આવર્તગતિનો આવર્તકાળ ......
- 3સમાન આવૃત્તિ અને સમાન કંપવિસ્તાર ધરાવતી બે પરસ્પર લંબ સરળ આવર્ત ગતિ વચ્ચે કળા તફાવત $ \frac{\pi }{2} $ છે, તો પરિણામી ગતિપથ કયા આકારનો થાય?View Solution
- 4અવમંદિત દોલકનો કંપવિસ્તાર $5$ $s$ તેના મૂળ મૂલ્યથી ઘટીને $0.9 $ ગણો થાય છે.બીજા $10$ $s$ ના અંતે તે તેના મૂળ મૂલ્યથી ઘટીને $\alpha $ ગણો બને છે.જયાં $\alpha $ = ______View Solution
- 5સ.આ.ગ. કરતાં કણનો કંપવિસ્તાર $3\,cm$ છે. સ્થાનાંતર ($cm$ માં) કે જ્યાં તેની ગતિઊર્જા સ્થિતિઉર્જા કરતાં $25 \%$ વધુ હશે?View Solution
- 6View Solutionસરળ આવર્તગતિ માટે સ્થાનાંતર વિરુઘ્ઘ સમયનો આલેખ આપેલ છે. કણ પર લાગતા બળ વિરુઘ્ઘ સમયનો આલેખ કેવો થાય?
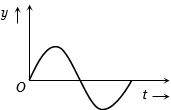
- 7જ્યારે કણ અંતિમ બિંદુ કરતાં અડધા અંતરે હોય ત્યારે સરળ આવર્ત ગતિ કરતાં કણની સ્થિતિ ઊર્જા કેટલી થાય? (જ્યાં $E$ કુલઊર્જા છે.)View Solution
- 8$x-$ અક્ષ પર મુક્ત રીતે ગતિ કરી શકતા કણની સ્થિતિ ઉર્જા $U(x) = k[1 - \exp {( - x)^2}]$ for $ - \infty \le x \le + \infty $ દ્વારા આપેલ છે. જ્યાં $k$ એ અનુરૂપ પરિમાણ માં ધન અચળાંક છે. તો.....View Solution
- 9એક પદાર્થ સરળ આવર્ત ગતિ કરે છે. જ્યારે તેનું સમતોલન સ્થાનથી સ્થાનાંતર $4\,cm $ અને $5\,cm$ હોય, ત્યારે પદાર્થનો તેને અનુરૂપ વેગ અનુક્રમે $10\,cm/sec$ અને $8\, cm/sec$ છે. તો પદાર્થનોઆવર્તકાળ કેટલો હશે?View Solution
- 10View Solutionએક ચિમ્પાન્ઝી(વાંદરો) હીંચકા પર બેસી ઝૂલા ખાય છે.જો ચિમ્પાન્ઝી ઊભો થઇને ઝૂલા ખાય,તો હીંચકાનો આવર્તકાળ...
