શ્રેણીમાં જોડેલી સમાન લંબાઇની બે કેશનળીની ત્રિજયાનો ગુણોત્તર $ 1:2 $ છે.તેના બે છેડા વચ્ચે દબાણનો તફાવત $1m$ ઊંચાઇના પાણીના સ્તંભ જેટલો છે.તો પ્રથમ કેશનળી વચ્ચે દબાણનો તફાવત ....... $m$ ઊંચાઇના પાણીના સ્તંભ જેટલો હોય.
Diffcult
d
(d)Given, \({l_1} = {l_2} = 1,\)and \(\frac{{{r_1}}}{{{r_2}}} = \frac{1}{2}\) \(V = \frac{{\pi {P_1}r_1^4}}{{8\eta l}} = \frac{{\pi {P_2}r_2^4}}{{8\eta l}}\)==> \(\frac{{{P_1}}}{{{P_2}}} = {\left( {\frac{{{r_2}}}{{{r_1}}}} \right)^4} = 16\) ==> \({P_1} = 16{P_2}\) Since both tubes are connected in series, hence pressure difference across combination, \(P = {P_1} + {P_2}\)==> 1 = \({P_1} + \frac{{{P_1}}}{{16}}\) ==> \({P_1} = \frac{{16}}{{17}} = 0.94m\)
(d)Given, \({l_1} = {l_2} = 1,\)and \(\frac{{{r_1}}}{{{r_2}}} = \frac{1}{2}\) \(V = \frac{{\pi {P_1}r_1^4}}{{8\eta l}} = \frac{{\pi {P_2}r_2^4}}{{8\eta l}}\)==> \(\frac{{{P_1}}}{{{P_2}}} = {\left( {\frac{{{r_2}}}{{{r_1}}}} \right)^4} = 16\) ==> \({P_1} = 16{P_2}\) Since both tubes are connected in series, hence pressure difference across combination, \(P = {P_1} + {P_2}\)==> 1 = \({P_1} + \frac{{{P_1}}}{{16}}\) ==> \({P_1} = \frac{{16}}{{17}} = 0.94m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\,cm \times 10 \,cm \times 15 \,cm$ કદનો એક લંબચોરસ બ્લોક $10 \,cm$ બાજુના શિરોલંબ સાથેના પાણીમાં તરે છે. જો તે $15 \,cm$ બાજુના શિરોબંબ સાથેના પાણીમાં તરે છે તો પાણીનું સ્તર .........View Solution
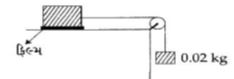
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે જેના પાયાનું ક્ષેત્રફળ $0.2 \;m^2$ હોય, તેવા એક બ્લેાકને $0.02 \;kg$ નું દળ એક દોરી વડે એક આદર્શ ગરગડી પરથી લગાડેલ છે. એક પ્રવાહીનું $0.6\; mm$ જાડાઈનું પાતળું સ્તર આ બ્લોક અને ટેબલ વચ્ચે મૂકવામાં આવે છે. જયારે બ્લોકને છોડવામાં આવે ત્યારે તે $0.17 \;m/s$ ની અચળ ઝડપથી જમણી તરફ ગતિ કરે છે. આ પ્રવાહીનો સ્નિગ્ધતાંક કેટલો હશે?View Solution
- 3$Viscosity$ એ પ્રવાહીનો એવો ગુણધર્મ છે જેથી $..............$View Solution
- 4સમાન ત્રિજયાના બે ટીપાં $5cm/sec$ ના વેગથી ગતિ કરતાં ભેગા થઇ જાય,તો મોટાં ટીપાંનો ટર્મિનલ વેગ કેટલો થાય?View Solution
- 5અનિયમિત આડછેદ ધરાવતી પાઇપમાં બે બિંદુએ ત્રિજયાનો ગુણોત્તર $3:2$ છે.તો વેગનો ગુણોત્તર કેટલો થાય?View Solution
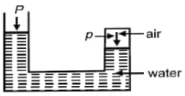
- 6મર્યાદિત હવાનું દબાણ $p$ છે. જો વાતાવરણનું દબાણ $P$ છે તો...View Solution
- 7ખુલ્લી $U$ આકારની ટ્યુબમાં મરક્યુરી ભરેલી છે. જ્યારે એક બાજુ $13.6 \,cm$ જેટલું પાણી ભરવામાં આવે તો આ પરિસ્થિતિએ મરક્યુરીના લેવલમાં ................. $cm$ વધારો થશે.View Solution
- 8$d _1$ અને $d _2$ ઘનતા ધરાવતા પ્રવાહી એ સમાન દબાણ તફાવત હેઠળ આદર્શ કેપિલરી ટ્યુબમાં વહે છે.પ્રવાહીનું સમાન પ્રમાણ (દળ) વહન કરવા માટે લાગેલો સમય $t _1$ અને $t _2$ હોય, પ્રવાહીના શ્યાનતા ગુણાંકનો ગુણોતર $......... $View Solution
- 9$d,\,2d$ અને $3d$ ઘનતા ધરાવતા ત્રણ પ્રવાહી સમાન દળ લઇને મિશ્રણ કરવાથી, મિશ્રણની ઘનતા કેટલી થાય?View Solution
- 10એક $H$ ઊંચાઈના મોટા પાતને, $\rho$ ઘનતાના પ્રવાહીથી છલોધલ ભરવામાં આવે છે. તેની શિરોલંબ બાજુની સપાટી પર $r$ ત્રિજ્યાનું એક નાનું છિદ્ર બનાવવામાં આવે છે. (તળિયાની એકદમ નજીક) તો પ્રવાહીના દબાણને રોકવા માટે જરરી સમક્ષિતિજ બળ કેટલું હશે ?View Solution
