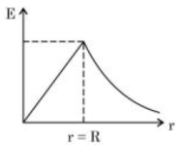
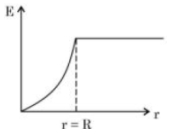
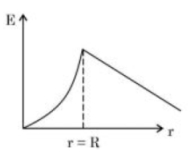
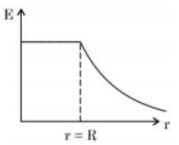
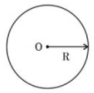
સમાન રીતે ભારીત અવાહક ધનગોળાના વીજક્ષેત્રના ફેરફારને વિવિધ બિંદુઓ આધારીત આલેખીય રીતે દર્શાવી શકાય છે.
- A
- B
- C
- D
JEE MAIN 2023, Medium
Download our app for free and get started
a
Electric field of solid sphere (uniformly charged)
Electric field of solid sphere (uniformly charged)
\(E( r ) \begin{cases}\frac{ Q }{4 \pi \in_0 r ^2} & r \geq R \\ \frac{ Qr }{4 \pi \in_0 R ^3} & r \leq R \end{cases}\)
Graphically
\(E(r) \propto r\) for \(r \leq R\)
\(\propto \frac{1}{r^2} \text { for } r \geq R\)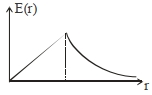
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમકેન્દ્રિય ગોળીય કવચ $A$ અને $B $ ની ત્રિજયાઓ $r_A$ અને $r_B(r_B>r_A)$ છે.તેના પર વિદ્યુતભાર $Q_A$ અને $-Q_B(|Q_B|>|Q_A|)$ છે.તો વિદ્યુતક્ષેત્ર વિરુધ્ધ અંતરનો નો આલેખ કેવો થાય?View Solution
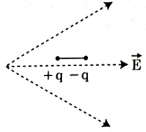
- 2View Solutionઆકૃતિમાં દર્શાવ્યા અનુસાર એક ડાયપોલને વિદ્યુતક્ષેત્રમાં મૂકવામાં આવે છે. તે કઈ દિશામાં ગતિ કરશે?
- 3હાઇડ્રોજનમાં એક ઇલેક્ટ્રોન ન્યુક્લિયસની ફરતે $r$ ત્રિજ્યાની વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે. તે બન્ને વચ્ચે લાગતું કુલંબ બળ $\overrightarrow F $ કેટલું હશે? ($K = \frac{1}{{4\pi {\varepsilon _0}}}$)View Solution
- 4$20$ યુનિટ ક્ષેત્રફળ ધરાવતી સપાટી $Y-Z$ સમતલમાં છે,જો વિદ્યુતક્ષેત્ર $(5 \hat{i}+4 \hat{j}+9 \hat{k})$ હોય તો સપાટીમાંથી પસાર થતું ફલક્સ શોધો. (એકમ માં)View Solution
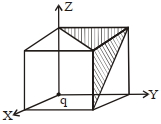
- 5આકૃતિમાં દર્શાવ્યા મુજબ $'q'$ વિજભાર ને સમઘનનાં એક ખૂણા પર ગોઠવવામાં આવ્યો છે. આચ્છાદિત ક્ષેત્રફળમાંથી પસાર થતાં સ્થિત વીજ ક્ષેત્ર $\overrightarrow{ E }$ નું ફ્લક્સ ...... હશે.View Solution
- 6અનંત ધનરેખીય વિદ્યુતભાર ફરતે $0.1 \,m$ ત્રિજ્યાના વર્તુંળમાં એક ઇલેક્ટ્રોન ભ્રમણ કરે છે. જો રેખીય વિદ્યુતભાર ઘનતા $1\,\mu C / m$, હોય, તો ઈલેક્ટોનનો વેગ $m / s$ માં ............. $\times 10^7$ છે.View Solution
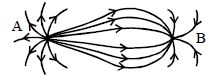
- 7બે વિધુતભાર $(A,\,B)$ દ્વારા ઉત્પન્ન થતી વિધુતક્ષેત્રરેખાનું વિતરણ આપેલ છે તો નીચેનામાથી કયું વિધાન સાચું થાય ?View Solution
- 8સમાન વિદ્યુતભાર ધરાવતા બે સમાન ગોળાઓને એક આધારબિંદુથી સરખી લંબાઈની દોરી વડે લટકાવેલ છે. ત્યારે બે દોરી વચ્ચેનો કોણ $30^o$ છે. જ્યારે $0.8\, g\, cm^{-3}$ ઘનતાના પ્રવાહીમાં ડૂબાડવામાં આવે ત્યારે બે દોરી વચ્ચેનો કોણ ગોળાઓ હવામાં હતા તયારે જેટલો હતો તેટલો જ રહે છે. જો ગોળાઓના દ્રવ્યની ઘનતા $1.6 \,g \,cm^{-3}$ હોય તો પ્રવાહીનો ડાઈઈલેક્ટ્રિક અચળાંક ........ છે.View Solution
- 9ગાઉસનો નિયમ ${ \in _0}\,\oint\limits_{} {\vec E,\,d\vec s\,\, = \,\,q} $ દ્વારા આપવામાં આવે છે જો ગાઉસિયન પૃષ્ઠ વડે ઘેરાતો ચોખ્ખો વિદ્યુતભાર શૂન્ય હોય તો .......View Solution
- 10$L$ લંબાઈ અને $R$ ત્રિજ્યાનો એક નળાકાર લો કે જેની અક્ષો વિદ્યુતક્ષેત્ર ને સમાંતર હોય નળાકાર સાથે સંકળાયેલ કુલ વિદ્યુત ફલક્સ ....... છે.View Solution