સમાન ત્રિજ્યાના એક નક્કર ગોળો અને તકતી ઢોળાવવાળી સપાટી પર લપસ્યા વગર પડે છે. એક એ બીજા કરતા વહેલા પહોંચે છે તેનું કારણ
Medium
a
(a)
(a)
\((i)\) For solid sphere, the moment of inertia about the diameter is \(I _{ s }=\frac{2}{5} MR ^2\)
Now \(I = MK ^2\) for any body, where \(K\) is radius of gyration of that body.
so \(MK ^2=\frac{2}{5} MR ^2 \Rightarrow K = R \sqrt{2 / 5}\)
\((ii)\) The moment of inertia of disc about an axis passing through its centre and perpendicular to plane is
\(I _{ d }=\frac{ MR ^2}{2}= MK ^2 \Rightarrow K = R \sqrt{1 / 2}\)
Now acceleration of any body which is rolling on an inclined plane is
\(a=\frac{g \sin \theta}{1+K^2 / R^2}\)
For same R, the acceleration of the body depends only on radius of gyration \(K\), [see eq\((iii)\)] so solid sphere will reach earlier to bottom of an inclined plane than disc.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$m$ દ્રવ્યમાન $ R$ ત્રિજયાનો એક ઘન ગોળો તેના વ્યાસને અનુલક્ષીને ચાકગતિ કરે છે. સમાન દ્રવ્યમાન અને સમાન ત્રિજયાનો એક નળાકાર પણ તેની ભૌમિતિક અક્ષને અનુલક્ષીને ગોળાની કોણીય ઝડપથી બમણી કોણીય ઝડપથી ગતિ કરે છે. આ બંનેની ચાકગતિ ઊર્જાઓનો ગુણોત્તર $E$ ગોળો$/E$ નળાકાર કેટલો થાય?View Solution
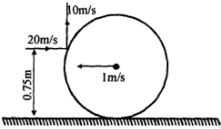
- 2$2\ kg$ પાતળી રિંગની ત્રિજ્યા $0.5\ m$ છે. તે $1\ m/s $ ના વેગથી સમક્ષિતિજ સમતલ પર સરક્યા વિના ગબડે છે. $0.1\ kg$ દળનો નાનો બોલ તેની વિરૂદ્ધ દિશામાં $20\ m/s$ ગના વેગથી ગતિ કરે છે અને રિંગને $ 0.75\ m$ ઉચાઈએ અથડાઈને શિરોલંબ દિશામાં $10\ m/s$ વેગથી ગતિ કરે છે. અથડામણની તરત જ બાદ....View Solution
- 3ફ્લાયવ્હીલની ઝડપ $60\,rpm$ થી $360\,rpm$ સુધી વધારવા માટે $484\,J$ જેટલી ઊર્જા ખર્ચવામાં આવે છે. ફ્લાયવ્હીલની જડત્વની ચાકમાત્રા $............\,kg - m ^2$ હશે.View Solution
- 4એક તક્તી $\vec{\omega}$ કોણીય ઝડપથી ભ્રમણ કરી રહી છે. બ્રમણાક્ષની સાપેક્ષે સ્થાન સદિશ $\vec{r}$ ધરાવતાં બિંદુ પર $\vec{F}$ બળ લગાડવામાં આવે છે. તો આ બળ વડે ઉદભવતાં ટોર્કની સાથે જોડાયેલો પાવર શું થશે ?View Solution
- 5$1\,kg$ દળ અને $R$ ત્રિજ્યયા ઘરાવતી તક્તિ તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ તેવી સમક્ષિતિજ અક્ષને અનુલક્ષીને પરિભ્રમણ કરવા મુક્ત છે. તક્તિ જેટલું દળ ધરાવતી વસ્તુને તક્તિનાં સૌથી ઉપરના છેડા આગળ જોડવામાં આવે છે. હવે આ તંત્રને છોડવામાં આવે છે, જયારે વસ્તુ સૌથી નીચેના છેડે આવે છે ત્યારે કોણીય ઝડપ $4 \sqrt{\frac{x}{3 R}} rad s ^{-1}$ થાય છે.$x$નું મૂલ્ય $.......$ થશે.View Solution
$[\left.g =10\,m / s ^{2}\right]$
- 6બે $0.3\ kg$ અને $0.7\ kg$ દળના પદાર્થને એક $1.4\ m$ લંબાઈની લાકડીના જેનું દળ નહિવત્ત છે તેના છેડે બાંધેલા છે. લાકડીને તેની લંબાઇની લંબ દિશામાં અચળ કોણીય વેગથી ફેરવવામાં આવે છે. ન્યૂનતમ કાર્યથી લાકડીને ફેરવવા માટે અક્ષ નું સ્થાન ક્યાં હોવું જોઈએ ?View Solution
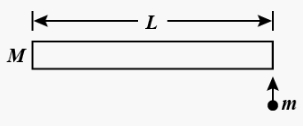
- 7એક $l$ લંબાઇની અને $M$ દળની લાકડી એક ઘર્ષણરહિત સમક્ષિતિજ સપાટી પર પડેલ છે. $v$ વેગથી ગતિ કરતો એક $ m$ દળનો દડો આકૃતિમાં દર્શાવ્યામુજબ સ્થિતિસ્થાપક સંઘાત અનુભવે છે. સંઘાત પછી દડો સ્થિર થાય તો તેનું દળ કેટલું હશે ?View Solution
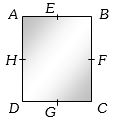
- 8એક લંબચોરસ $ABCD \,(BC=2AB)$ માં ન્યૂનતમ જડત્વની ચાકમાત્રા કઈ અક્ષને અનુલક્ષીને હોય?View Solution
- 9$1 \,\,g, 2 \,\,g$ અને $3\,\, g$ દળ ધરાવતા કણોથી બનેલા તંત્રનું દ્રવ્યમાન કેન્દ્ર ઊગમબિંદુ પર છે. $4 \,\,g$ દળ અને $\alpha (\hat i + 2\hat j + 3\hat k)$ સ્થાનસદિશ ધરાવતા કણને સામેલ કરતાં તંત્રના દ્રવ્યમાન કેન્દ્રના યામ $(1, 2, 3)$ મળે છે. જો અચળ હોય, તો તેનું મૂલ્ય ..... હોવું જોઈએ.View Solution
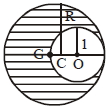
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $\mathrm{R}$ ત્રિજ્યાના ગોળામાથી $1$ ત્રિજ્યાનો ગોળો કાપી નાખવામાં આવેલ છે વધેલા ભાગનું દ્રવ્યમાનકેન્દ્ર $G$ આગળ મળતું હોય તો $R$ કયા સમીકરણ વડે મેળવી શકાય?View Solution