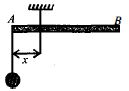
આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $\mathrm{R}$ ત્રિજ્યાના ગોળામાથી $1$ ત્રિજ્યાનો ગોળો કાપી નાખવામાં આવેલ છે વધેલા ભાગનું દ્રવ્યમાનકેન્દ્ર $G$ આગળ મળતું હોય તો $R$ કયા સમીકરણ વડે મેળવી શકાય?
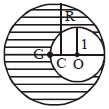

JEE MAIN 2020, Diffcult
c
By concept of \(COM\)
By concept of \(COM\)
\(\mathrm{m}_{1} \mathrm{R}_{1}=\mathrm{m}_{2} \mathrm{R}_{2}\)
Remaining mass \(\times(2-\mathrm{R})=\) cavity mass \(\times(\mathrm{R}-1)\)
\(\left(\frac{4}{3} \pi \mathrm{R}^{3} \rho-\frac{4}{3} \pi l^{3} \rho\right)(2-\mathrm{R})=\frac{4}{3} \pi l^{3} \rho \times(\mathrm{R}-1)\)
\(\left(\mathrm{R}^{3}-1\right)(2-\mathrm{R})=\mathrm{R}-1\)
\(\left(\mathrm{R}^{2}+\mathrm{R}+1\right)(2-\mathrm{R})=1\)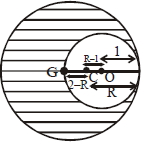
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionપાતળી પોલો નળાકાર બંનેને છેડેથી ખુલ્લો છે. તે રોલિંગ કર્યા વિના સરકે છે અને પછી સરક્યા વિના તેટલી જ ઝડપથી રોલિંગ કરે છે બંને કિસ્સામાં ગતિ ઊર્જાનો ગુણોત્તર ........ થશે.
- 2એક હળવી દોરીને $5\,kg$ દળ અને $70\,cm$ ત્રિજ્યા ધરાવતા એક પોલા નળાકારની આસપાસ વીટાળવામાં આવે છે. દોરીને $52.5\,N$ બળ વડે ખેંચવામાં આવે છે. નળાકારનો કોણીય પ્રવેગ .......... $rad\,s ^{-2}$ હશે.View Solution
- 3View Solutionઘન ગોળો,ઘન નળાકાર,તકતી અને રીંગ ઢાળ પર મૂકતાં તળિયે એકસાથે કોણ આવશે?
- 4$R$ અને $ nR$ ત્રિજ્યાની બે સમાન રિંગના કેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રાનો ગુણોત્તર $1 : 8$ છે. તો $ n$ ની કિંમત શું થશે ?View Solution
- 5$m$ દળ અને $R$ ત્રિજ્યાનો એક પોલો ગોળો એ $\theta$ ખૂણાવાળાં ઢોળાવયુક્ત ખરબચડા સમતલ પર ગબડે છે. જો પોલો ગોળો અને ઢોળાવ વચ્ચેનો ઘર્ષણાંક નીચે તરફ ગબડે $\mu$ હોય તો,View Solution
- 6View Solutionબે સમાન કદ, આકાર અને વજનના ઇંડા ક્રમમાં મૂકેલા છે. જેમાં એક કાચું અને બીજું અડધું બાફેલું છે. તો કેન્દ્રિય અક્ષ પર કાચા ઇંડા અને અડધા બાફેલા ઇંડાની જડત્વની ચાકમાત્રનો ગુણોત્તર કેટલો થશે ?
- 7કોઈ સમક્ષિતિજ સમતલ તેના કેન્દ્રમાથી પસાર થતી શિરોલંબ અક્ષને અનુલક્ષીને નિયમિત કોણીય વેગથી ભ્રમણ કરે છે. કોઈ ક્ષણે $m$ દળના ઘટ્ટ પ્રવાહીને તેના કેન્દ્ર પર પાડતા તે ફેલાઈને નીચે પડે છે. આ દરમિયાન તેનો કોણીય વેગમાં શું થશે?View Solution
- 8જો $\mathop {\rm{F}}\limits^ \to \, = \left( {\,4\hat i- 10\hat j\,} \right)$ અને $\mathop r\limits^ \to = \left( {\,5\hat i- 3\hat j\,} \right)$ હોય તો $\left( {\,\mathop \tau \limits^ \to = \mathop r\limits^ \to \times \mathop F\limits^ \to } \right)$ ની ગણતરી ... થાયView Solution
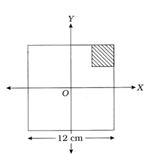
- 9આકૃતિમાં દર્શાવેલ $12\ cm$ લંબાઈની ચોરસ તકતીના એક ખૂણા પરથી $2\ cm $ લંબાઈનો એક ચોરસ કાપી લેવામાં આવે તો બાકી રહેતા ભાગનું દ્રવ્યમાન-કેન્દ્ર, મૂળ ચોરસના કેન્દ્રના સંદર્ભમાં કયાં હશે ? તકતી નિયમિત જાડાઈ અને ઘનતાની છે.View Solution
- 10આકૃ તિ માં દર્શાવ્યા મુજબ એક નિયમિત સળિયા $AB$ ને $A$ થી કોઈ ચલિત અંતર $X$ આગળ લટકાવેલો છે. સળિયાને સમક્ષિતિજ ગોઠવવા માટે દળ $m$ ને તેના છેડા $A$ સાથે લટકાવેલ છે. $(m, x)$ ની કિંમતો આપેલ છે. તેનો ગ્રાફ સુરેખા મળે તેના માટે ના ચલ શું હોય શકે?View Solution