સમાન વિદ્યુતક્ષેત્ર $\overrightarrow {\;E} $ ની અસર નીચે સમક્ષિતિજ $q$ વીજભારિત એક રમકડાંની કાર ઘર્ષણરહિત સપાટ સમક્ષિતિજ સમતલ પર ગતિ કરે છે.બળ $q \overrightarrow {\;E} $ ના કારણે એક સેકન્ડના ગાળામાં તેનો વેગ $0$ થી $6 \,m/s$ વધે છે. આ ક્ષણે આ ક્ષેત્રની દિશા ઉલટાવવામાં આવે છે. આ ક્ષેત્રની અસરમાં આ કાર બે સેકન્ડ ગતિ કરવાનું ચાલુ રાખે છે. $0$ થી $3$ સેકન્ડ વચ્ચે રમકડાની આ કારનો સરેરાશ વેગ અને સરેરાશ ઝડપ અનુક્રમે કેટલી હશે?
NEET 2018, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
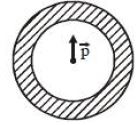
- 1આપેલ આકૃતિમાં દર્શાવેલ પોલા ગોળાની અંદરની ત્રિજ્યા $a$ અને બહારની ત્રિજ્યા $b$ છે જેના પર $Q$ વિદ્યુતભાર છે.તેના કેન્દ્ર પર આકૃતિમાં દર્શાવ્યા પ્રમાણે ડાયપોલ $\vec P$ હોય તો.....View Solution
- 2$9.0\, cm$ ની ધારવાળા એક ઘનાકાર ગોસિયન સપાટીના કેન્દ્ર પર $2.0\; \mu \,C$ વિદ્યુતભાર રહેલો છે. આ સપાટીમાંથી કુલ વિદ્યુત ફલક્સ કેટલું હશે?View Solution
- 3$M$ દળ અને $q$ વિજભાર $k$ દળ ધરાવતી સ્પ્રિંગ સાથે જોડાયેલ છે. $x = 0$ ને સમતોલન સ્થાન રાખીને તે $x-$દિશામાં $A$ કંપવિસ્તારથી દોલનો કરે છે,$x-$દિશામાં $E$ જેટલું વિદ્યુતક્ષેત્ર પ્રવર્તે છે. તો નીચેનામાંથી કયું વિધાન સાચું પડે?View Solution
- 4એક વિદ્યુતભાર $Q$ બે ભાગ $Q_1$ અને $Q_2$ માં વહેચાય છે. આ વિદ્યુતભારો $R$ અંતરે મૂકેલા છે. તેઓ વચ્ચેનું મહત્તમ અપાકર્ષી બળ માટે $Q_1$ અને $Q_2$ શું હશે ?View Solution
- 5ધન વિદ્યુતભારીત અને અનંત લંબાઈ ધરાવતા સીધા ધાગા ( દોરી) ની રેખીય વિદ્યુતભાર ધનતા $\lambda \mathrm{Cm}^{-1}$ છે. એક ઈલેક્ટ્રોન તેની અક્ષ પરની લંબાઈની દિશામાં રહે તે રીતે વર્તુળાકાર પથપર ભ્રમણ કરે છે. ઈલેક્ટ્રોનની તાર થી વર્તુળાકર પથની ત્રિજ્યાં વિધેય તરીકે ઉર્જાનો ફેરફાર. . . . . . . દ્વારા સાચી રીતે રજૂ કરી શાકાયView Solution
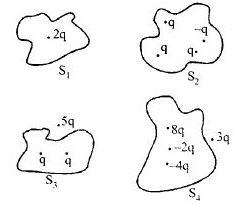
- 6ચાર સપાટી માટે વિદ્યુતભારનું વિતરણ આપેલ છે. તેમને અનુરૂપ વિદ્યુત ફ્લક્સ ${\phi _1},{\phi _2},{\phi _3}$ અને ${\phi _4}$ હોય તો નીચેનામાંથી શું સાચું પડે?View Solution
- 7$10^{-4} \mathrm{~m}^2$ આડછેદનું ક્ષેત્રફળ ધરાવતા પાતળા ધાતુના તારનો $30 \mathrm{~cm}$ ત્રિજયાની વલય બનાવવામાં ઉપયોગ થાય છે. $2 \pi \mathrm{C}$ મૂલ્યનો ધન વીજભાર સમાન રીતે વલય પર વિતરીત થયેલ છે જ્યારે $30 \mathrm{pC}$ મૂલ્યનો ધન વીજભાર વલયના કેન્દ્ર પર રાખેલ છે. વલયમાં ઉદભવતું તણાવબળ_____$\mathrm{N}$ છે કે જેને લીધે વલયમાં વિકૃતિ ઉદ્ભવતી નથી. (ગુરૂત્વીય અસર અવગણો)$\left(\right.$ ને, $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \mathrm{SI}$ એકમ $)$View Solution
- 8બે વિદ્યુતભાર $9e$ અને $3e$ ને $r$ અંતરે મૂકેલા છે,તો વિદ્યુતક્ષેત્ર શૂન્ય કયા થાય?View Solution
- 9$\rho (r)\,\, = \,\,{\rho _0}\left( {\frac{5}{4}\, - \,\,\frac{r}{R}} \right)$ એ વિદ્યુતભારની ઘનતા સાથે બદલાતું ગોળીય સંમિત વિદ્યુતભારનું વિતરણ આપે છે. જે $r = R$, અને $\rho (r)\,\, = \,\,0$ માટે $r > R$ જ્યાં $r$ એ ઉગમબિંદુથી અંતર છે. ઉગમબિંદુથી $r$ અંતરે $(r < R)$ વિદ્યુતક્ષેત્ર ....... દ્વારા આપવામાં આવે છે.View Solution
- 10એક ચોકકસ વિસ્તારમાં વિદ્યુતક્ષેત્ર $ E=Ar$ છે અને તે ત્રિજયાવર્તી દિશામાં બહાર તરફ છે. $a$ ત્રિજયાના ગોળાના કેન્દ્ર પર રહેલા વિદ્યુતક્ષેત્રથી ગોળા પર કેટલો વિદ્યુતભાર મળે?View Solution