સમાંતર પ્લેટ કેપેસીટર પર $50\, {Hz}$ આવૃતિવાળો $AC$ વોલ્ટેજ $V(t)=20\,sin\omega \,t$ લગાવવામાં આવે છે. બે પ્લેટ વચ્ચેનું અંતર $2\, {mm}$ અને ક્ષેત્રફળ $1 \,{m}^{2}$ છે. લગાવેલ $AC$ વોલ્ટેજ માટે સ્તહનાંતર પ્રવાહનો કંપવિસ્તાર ($\mu {A}$ માં) કેટલો થાય?
[$\left.\varepsilon_{0}=8.85 \times 10^{-12} \,{F} / {m}\right]$
JEE MAIN 2021, Diffcult
d
From the given information,
From the given information,
\({C}=\frac{\epsilon_{0} {A}}{{d}}={k} \frac{\epsilon_{0} \times 1}{2 \times 10^{-3}} {F}\)
\(\therefore {X}_{{c}}=\frac{1}{\omega {C}}=\frac{2 \times 10^{-3}}{2 \times 50 \pi {\epsilon}_{0}}=\frac{2 \times 10^{-3}}{25 \times 4 \pi \epsilon_{0}} \Omega\)
\(\therefore {X}_{{c}}=\frac{2 \times 10^{-3}}{25} \times 9 \times 10^{9}=\frac{18}{25} \times 10^{6} \Omega\)
\(\therefore {i}_{0}=\frac{{V}_{0}}{{X}_{{c}}}=\frac{20 \times 25}{18} \times 10^{-6} {A}=27.47 \mu {A}\)
The value of amplitude of displacement current will be same as value of amplitude of conventional current.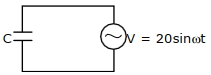
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વિદ્યુતચુંબકીય તરંગ $ k $ ડાઇઇલેકટ્રીક અને $ {\mu _r} $ સાપેક્ષ પરમીએબીલીટી ઘરાવતા માઘ્યમમાં પસાર થાય ત્યારે તેનો વેગ કેટલો થાય?View Solution
- 2View Solutionવિદ્યુતચુંબકીય તરંગો માટે નીચેનામાંથી ખોટું વિધાન પસંદ કરો.
- 3View Solutionનીચેનામાથી કયા વિધુતચુબકીય તરંગ નથી
- 4$10\, m$ અંતરે $8\, W$ પ્રકાશનાં ગોળામાંથી ઉત્સર્જાતા વિકિરણને કારણે ઉત્પન્ન મહત્તમ વીજક્ષેત્ર $\frac{x}{10} \sqrt{\frac{\mu_{0} c }{\pi}} \,\frac{ V }{ m }$ પ્રકારનાં ગોળાની કાર્યક્ષમતાં $10\, \%$ છે અને તે બિંદુવત્ સ્ત્રોત છે. તો $x$ નું મૂલ્ય ...... છે.View Solution
- 5View Solutionવિધુત ચુંબકીય તરંગના જુદા જુદા ભાગની તરંગ લંબાઈ વચ્ચેનો સબંધ
- 6સૂચિ $-I$ અને સૂચિ $-II$ ને મેળવો.View Solution
સૂચિ $-I$ સૂચિ $-II$ $(a)$ પારજાંબલી કિરણ $(i)$ સ્ફટિકનું બંધારણનો અભ્યાસ $(b)$ માઇક્રો (સૂક્ષ્મ) તરંગો $(ii)$ ગ્રીન હાઉસ અસર $(c)$ પારરક્ત તરંગો $(iii)$ વાઢકાપના ઓજારને શુધ્ધ કરવા $(d)$ $X$-કિરણો $(iv)$ રડાર તંત્ર નીચે આપેલ વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 7એક ધાતુમાં $X-$ દિશામાં $J_x$ ઘનતા ધરાવતો પ્રવાહ વહે છે તેને $B_z$ ($z-$ દિશામાં)જેટલા ચુંબકીયક્ષેત્રમાં મુકેલ છે. તેમાં $Y-$દિશામાં $E_y$ જેટલું વિદ્યુતક્ષેત્ર ઉત્પન્ન થાય છે જે $J_x$ અને $B_z$ ના સમપ્રમાણમાં છે.તો તેના માટેના સમપ્રમાણતા અચળાંકનો $SI$ એકમ શું થશે?View Solution
- 8જો $\overrightarrow E $ અને $\overrightarrow B $ અનુક્રમે વિદ્યુતચુંબકીય તરંગના વિદ્યુતક્ષેત્ર અને ચુંબકીયક્ષેત્ર સદીશ હોય, તો વિદ્યુતચુંબકીય તરંગના પ્રસરણની દિશા નીચેનામાંથી કઈ હશે?View Solution
- 9$+z$ દિશામાં ગતિ કરતાં વિદ્યુતચુંબકીય તરંગ માટે આવૃતિ $1\times10^{14}\, hertz$ અને વિદ્યુતક્ષેત્રનું મૂલ્ય $4\, V/m$ છે. જો ${\varepsilon_0}=\, 8.8\times10^{-12}\, C^2/Nm^2$ હોય તો આ વિદ્યુતક્ષેત્રની સરેરાશ ઉર્જા ઘનતા કેટલી હશે?View Solution
- 10View Solutionઓઝોન સ્તરની જૈવિક ઉપયોગિતા કઈ છે?
