State the midpoint theorem.
Download our app for free and get started
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View SolutionState Pythagoras theoram.
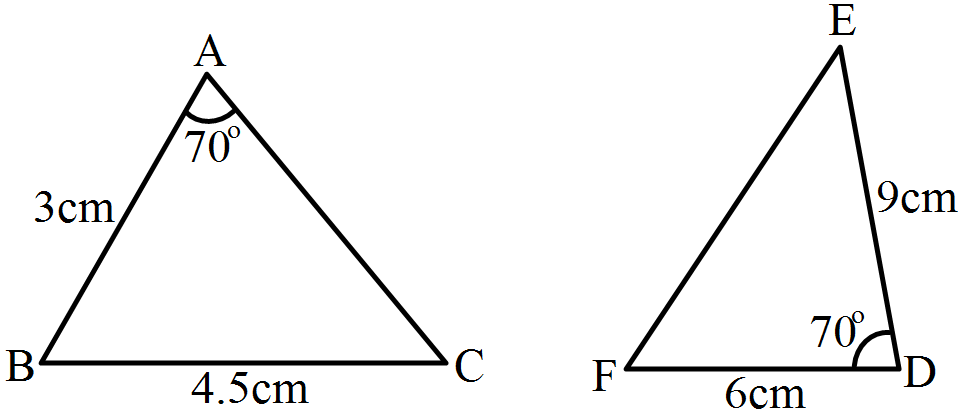
- 2View SolutionIn the given pairs of triangles, find which pair of triangles are similar. State the similarity criterior and write the similarity relation in symbolic from.
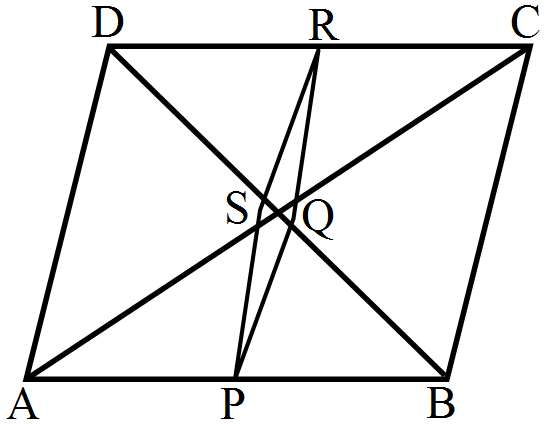
- 3View SolutionABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the midpoints of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
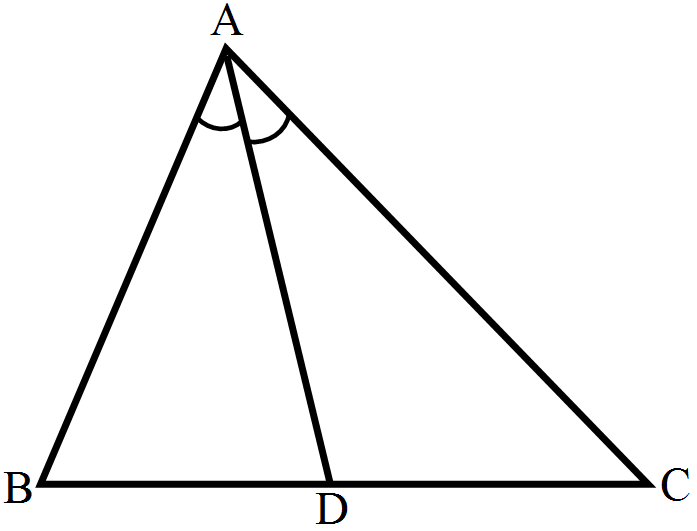
- 4In a $\triangle\text{ABC},\text{AD}$ is the bisector of $\angle\text{A}.$View Solution
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.
- 5ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that $\text{CQ}=\frac{1}{4}\text{AC}.$ If PQ produced meets BC at R, prove that R is the midpoint of BC.View Solution
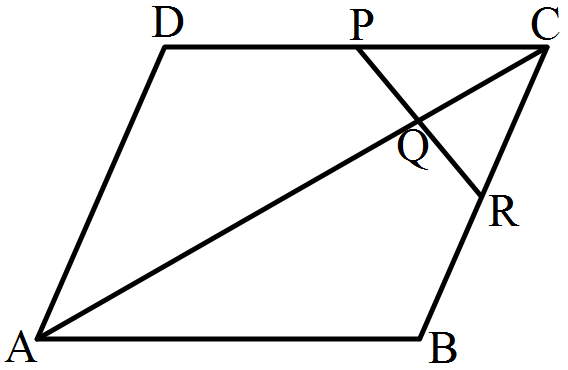
- 6View SolutionIn the given pairs of triangles, find which pair of triangles are similar. State the similarity criterior and write the similarity relation in symbolic from.
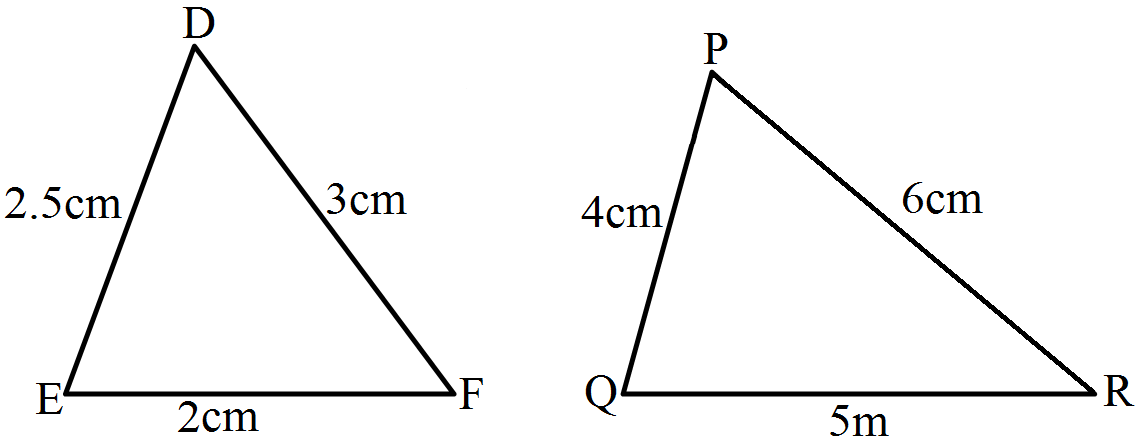
- 7View SolutionThe sides of certain triangles are given below. Determine them are right triangles:
9cm, 16cm, 18cm. - 8In the given figure, $\angle\text{CAB}=90^\circ$ and $\text{AD}\perp\text{BC}.$ Show that $\triangle\text{BDA}\sim\triangle\text{BAC}.$ If AC = 75cm, AB = 1m, and BC = 1,25m find AD.View Solution
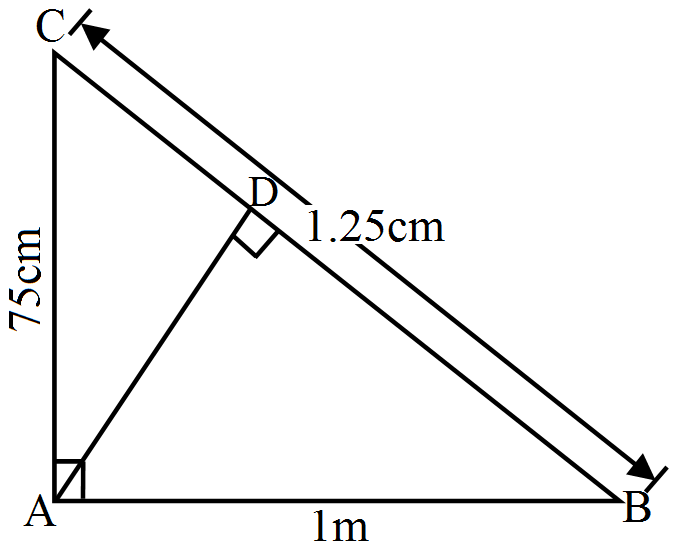
- 9View SolutionFind the height of an equilateral triangle of side 12cm.
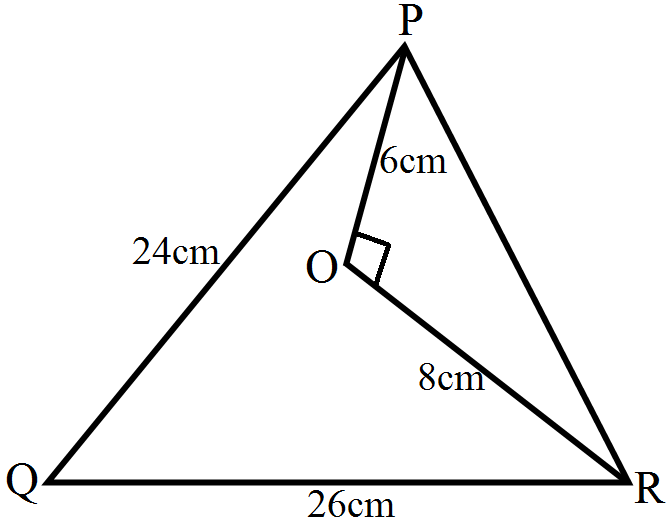
- 10In the given figure, O is a point inside a $\triangle\text{PQR}$ such that $\angle\text{PQR}=90^\circ,\text{OP}=6\text{cm}$ and $\text{OR}=8\text{cm}.$ If $\text{PQ}=24\text{cm}$ and $\text{QR}=26\text{cm},$ prove that $\triangle\text{PQR}$ is right-angled.View Solution
