સૂચિ List $-I$ ને સૂચિ List $-II$ સાથે મેળવો
| સૂચિ $-I$ | સૂચિ $-II$ |
| $(A)$ $R$ ત્રિજ્યા ધરાવતા ધન ગોળાની તેના કોઈપણ સ્પર્શકને અનુરૂપ જડત્વની ચાકમાત્રા | $(I)$ $\frac{5}{3} MR ^{2}$ |
| $(B)$ $R$ ત્રિજ્યા ધરાવતા પોલા ગોળાની તેના કોઈપણ સ્પર્શકને અનુરૂપ જડત્વની ચાકમાત્રા | $(II)$< $\frac{7}{5} MR ^{2}$ |
| $(C)$ $R$ ત્રિજ્યા ધરાવતી વર્તુળાકાર રીંગની તેના વ્યાસને અનુરૂપ જડત્વની ચાકમાત્રા | $(III)$ $\frac{1}{4} MR ^{2}$ |
| $(D)$ $R$ ત્રિજ્યા ધરાવતી વર્તુળાકાર તક્તિની કોઈપણ વ્યાસને અનુરૂપ જડત્વની ચાકમાત્રા | $(IV)$ $\frac{1}{2} MR ^{2}$ |
JEE MAIN 2022, Medium
a
\(I _{0}= I _{ com }+ MR ^{2}\)
\(I _{0}= I _{ com }+ MR ^{2}\)
(Parallel Axis theorem)
\(I_{0}=\frac{2}{5} M^{2}+M^{2}\)
\(I_{0}=\frac{7}{5} M R^{2}\)
Hollow sphere
\(I_{0}=I_{\text {com }}+M^{2}\)
\(=\frac{2}{3} M^{2}+M^{2}=\frac{5}{3} M^{2}\)
\(I _{1}+ I _{2}+ I _{3}\) (Perpendicular axis theorem)
By symmetry MOI
About \(1"\) and \(2"\) Axis are same i.e.
\(I _{1}= I _{2}\)
\(\therefore 2 I_{1}=I_{3}=M^{2}\left(I_{\text {com }}=M^{2}\right)\)
\(I_{1}=\frac{M R^{2}}{2}\)
Similarly in disc
\(2 I_{1}=\frac{M R^{2}}{2}\left\{I_{\text {com }}=\frac{M^{2}}{2}\right\}\)
\(I _{1}=\frac{ MR ^{2}}{4}\)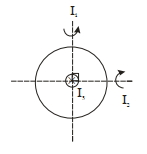
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનિયમિત વર્તૂળગતિ કરતા કણની રેખીય ઝડપ ચાર ગણી કરવામાં આવે અને કોણીય વેગ બમણો કરવામાં આવે, તો કણનો કેન્દ્રગામી પ્રવેગ .....
- 2$5\,kg$ નક્કર દળનો ગોળો અને $4\,kg$ દળની તકતી સમાન ત્રિજ્યા ધરાવે છે. તકતીની સમતલમાં સ્પર્શકમાંથી પસાર થતી અને નક્કર ગોળાના સ્પર્શકમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રાનો ગુણોત્તર $\frac{x}{7}$ હોય, તો $x$ નું મૂલ્ય $..............$ થાય.View Solution
- 3$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી એક તકતીની તેના વ્યાસને અનુલક્ષીને જડત્વની ચાક્માત્રા $\frac{ MR ^2}{4}$ છે. તકતીને લંબ અને તેના છેડાના બિંદુમાંથી પસાર થતી અક્ષને અનુલક્ષીને આ તકતીની જડત્વની ચાક્માત્રા $\frac{ x }{2} MR ^2$ મળે છે. $x$ નું મૂલ્ય $.........$ થશે.View Solution
- 4એક તકતી $\omega$ કોણીય ઝડપથી ભ્રમણ કરે છે. જો એક બાળક તેના પર બેસેલું હોય, તો નીચેનામાથી શેનું સંરક્ષણ થાય?View Solution
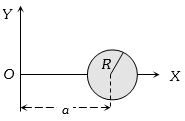
- 5$X-Y$ સમતલમાં આકૃતિ માં દર્શાવ્યા પ્રમાણે $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતી $X$ અક્ષ પર મુકેલી છે $X$ અક્ષ ને અનુલક્ષીને તકતીની જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
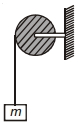
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે $m$ દળ અને $r$ ત્રિજ્યા વાળી એક તક્તી તેના કેન્દ્રને અનુલક્ષીને મુક્તપણે ભ્રમણ કરે છે. તેના ધાર પર એક દોરી વિંટાળવામાં આવે છે અને $m$ દળનો એક બ્લોક દોરીના મુક્ત છેડે જોડવામાં આવે છે. તંત્ર ને સ્થિરમાંથી મુક્ત કરવામાં આવે છે. જ્યારે બ્લોક $h$ ઊંચાઈથી નીચે તરફ ગતિ કરે છે ત્યારે બ્લોકની ઝડપ શોધો.View Solution
- 7$L$ લંબાઇનો સળિયા બે માણસના ખંભા પર છે. છેડા પરના એક માણસ પર $ 1\over 4 $ માં ભાગનું વજનબળ લાગે છે. તો બીજો માણસ આ છેડાથી કેટલે દૂર હશે?View Solution
- 8View Solutionસમાન દળ અને ત્રિજ્યાની રિંગ અને ધન ગોળો તેના વ્યાસાંત અક્ષ પર સમાન કોણીય વેગથી ચાકગતિ કરે છે, ત્યારે....
- 9$1 \,\,g, 2 \,\,g$ અને $3\,\, g$ દળ ધરાવતા કણોથી બનેલા તંત્રનું દ્રવ્યમાન કેન્દ્ર ઊગમબિંદુ પર છે. $4 \,\,g$ દળ અને $\alpha (\hat i + 2\hat j + 3\hat k)$ સ્થાનસદિશ ધરાવતા કણને સામેલ કરતાં તંત્રના દ્રવ્યમાન કેન્દ્રના યામ $(1, 2, 3)$ મળે છે. જો અચળ હોય, તો તેનું મૂલ્ય ..... હોવું જોઈએ.View Solution
- 10એક ચક્ર સ્થિર સ્થિતિમાંથી શરૂ થઈને $20 \,s$ માટે $2 \,rad / s ^2$ નાં નિયમિત દરથી પ્રવેગિત થાય છે. તેને બીજી $10 \,s$ માટે એજ નિયમિત પ્રવેગ સાથે ભ્રમણ કરવાની છુટ આપવામાં આવે છે અને તે અંતે ત્યારબાદની $20 \,s$ સ્થિર થાય છે. ચક્ર દ્વારા કુલ ભ્રમણ થયેલો ખૂણો (રૂડીયનમાં) કેટલો થાય?View Solution
