As it starts from rest,
we have, \(x=A \cos \omega t .\) At \(t=0, x=A\)
When \(t=\tau, x=A-a\) and
\(\text { when } t=2 \tau, x=A-3 a\)
\(\Rightarrow A-a=A \times \cos \times \omega \tau\) and \(...(i)\)
\(A-3 a=A \times \cos \times 2 \omega \tau\) \(...(ii)\)
As, \(\cos 2 \omega \tau=2 \cos ^{2} \omega \tau-1\)
\(\Rightarrow \quad \frac{A-3 a}{A}=2\left(\frac{A-a}{A}\right)^{2}-1\)
\(\therefore \quad \frac{A-3 a}{A}=\frac{2 A^{2}+2 a^{2}-4 A a-A^{2}}{A^{2}}\)
\(\therefore \quad A^{2}-3 a A=A^{2}+2 a^{2}-4 A a\)
\(\therefore \quad a^{2}=2 a A \Rightarrow A=2 a\)
\(\text { Now, } A-a=A \times \cos \times \omega \tau \ldots \ldots[\text { From }(1)]\)
\(\Rightarrow \quad \cos x \omega \tau=\frac{1}{2}\)
\(\therefore \quad \frac{2 \pi}{T} \tau=\frac{\pi}{3} \Rightarrow T=6 \tau\)
Download our appand get started for free
Similar Questions
- 1$90 \,J$ જેટલી કંપનગતિની ઊર્જા અને $6 \,cm$ નો કંપવિસ્તાર ધરાવતી સરળ આવર્તગતિ એક કણ કરી રહ્યો છે. જ્યારે તે કણ મધ્યબિંદુુથી $4\, cm$ અંતરે પહોંચે છે. ત્યારે એક ક્ષણ માટે રોકીને છોડવામાં આવે છે. હવે તેનાં દોલનની નવી ઉર્જા ......... $J$ થશે.View Solution
- 2દોરી વડે લટકાવેલ એક બોલ શિરોલંબ સમતલમાં એવી રીતે ગતિ કરે છે કે જેથી તેના અત્યંત બિંદુ અને સૌથી નીચેનાં બિંદૂ આગળ પ્રવેગનું મૂલ્ય સમાન રહે. અંત્ય બિંદુ આગળ માટે દોરીનાં આવર્તન કોણ $(\theta)$_____થશે.View Solution
- 3$m$ દળવાળો પદાર્થ $ {x_1} $ અને $ {x_2} $ બિંદુ વચ્ચે સરળ આવર્ત ગતિ થાય છે, તેનું સમતોલન સ્થાન $O$ છે. તેની સ્થિતિઊર્જા નીચે આપેલા કયા આલેખ વડે આપી શકાય?View Solution
- 4નીચે દર્શાવેલ સમીકરણોમાં કયું સમીકરણ સ.આ.ગ. દર્શાવે છે?View Solution
$(A)\;y= sin\omega t-cos\omega t$
$(B)\;y=sin^3\omega t$
$(C)\;y=5cos\left( {\frac{{3\pi }}{4} - 3\omega t} \right)$
$(D)\;y=1+\omega t+{\omega ^2}{t^2}$
- 5View Solutionજ્યારે કણ સ.આ.ગ. કરતો હોય તો વેગનું સ્થાનાંતરના વિધેયમાં (પદમાં) આલેખીય નિરૂપણ ..... થશે.
- 6સરળ આવર્ત ગતિ કરતાં પદાર્થનો કંપવિસ્તાર $4 \,cm$ છે,સમતોલન સ્થાન પાસે વેગ $16\, cm/s$ હોય,તો કયાં સ્થાન આગળ વેગ $ 8\sqrt 3\, cm/s, $ થાય? ..... $cm$View Solution
- 7$m$ દળ અને $A$ આડછેદ ધરાવતા લંબઘન બ્લોક $\rho$ ઘનતા ધરાવતા પ્રવાહીમાં તરે છે, તેને સમતોલન સ્થિતિમાંથી સૂક્ષ્મ શિરોલંબ સ્થાનાંતર કરાવતા તેની સરળ આવર્તગતિનાં આવર્તકાળ $T$ હોય તો ...View Solution
- 8એક સ્પ્રિંગ સાથે જોડેલા અને સરળ આવર્તગતિ કરતા પદાર્થના સ્થાનાંતરનું સમીકરણ $x =2 \times 10^{-2} \cos \pi t$ મીટર છે. પ્રથમ વખત મહત્તમ ઝડપ પ્રાપ્ત કરવા કેટલો સમય ($sec$ માં) લાગશે?View Solution
- 9સરળ આવર્તગતિનો મહતમ કંપવિસ્તાર($cm$ માં) કે જેથી બ્લોક $A$ બ્લોક $B$ બ્લોક પર ખસે નહીં $(K =100 N / m)$View Solution
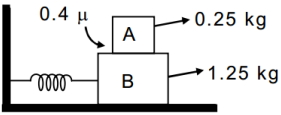
- 10એક પદાર્થ $‘n'$ આવૃત્તિ સાથેની સરળ આવર્ત ગતિ કરે છે, તેની સ્થિતિઊર્જાની આવૃત્તિ $....$ હશે.View Solution
