સૂર્ય અને પૃથ્વી વચ્ચેનું અંતર $2 \times 10^{8}\, km,$ સૂર્યનું તાપમાન $6000\, K ,$ સૂર્યની ત્રિજયા $7 \times 10^{5}\, km.$ જો પૃથ્વીની ઉત્સર્જકતા $0.6$ હોય તો ઉષ્મીય સંતુલન માટે પૃથ્વીનું તાપમાન ($K$ માં) થશે?
AIIMS 2019, Medium
b
For the condition of thermal equilibrium the energy received by earth should be equal to the energy transmitted by earth.
For the condition of thermal equilibrium the energy received by earth should be equal to the energy transmitted by earth.
\(\frac{T_{ s }^{4} 4 \pi R_{ s }^{2}}{4 \pi d^{2}} \times \pi R_{e}^{2}=\sigma \rho T_{e}^{4} 4 \pi R_{e}^{2}\)
\(T_{c}^{4}=\frac{T_{ s }^{4} R_{ s }^{2}}{4 e d^{2}}\) \(....(I)\)
Substitute \(6000\) for \(T_{s}, 7 \times 10^{8}\) for \(R_{5}, 2 \times 10^{11}\) for \(d\) and \(0.6\) for \(e\) in equation \((I).\)
\(T_{ e }^{4}=\frac{(6000)^{4}\left(7 \times 10^{8}\right)^{2}}{4\left(2 \times 10^{11}\right)^{2} \times 0.6}\)
\(=\frac{36 \times 36 \times 7 \times 7}{4 \times 4 \times 0.6} \times 10^{6}\)
\(=66.15 \times 108\)
\(T_{ e } \approx 300 K\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ગરમ પાણીનું તાપમાન $ {100^o}C $ થી $ {70^o}C $ થતા $4 min$ લાગે છે,તો તાપમાન $ {70^o}C $ થી $ {40^o}C $ થતા લાગતો સમય ....... $\min.$ થાશે.. વાતાવરણનું તાપમાન $ {15^o}C $ છેView Solution
- 2જો સૂર્યનું તાપમાન કદાચ $T$ થી વધીને $2\,T$ થાય અને તેની ત્રિજયા $R$ થી વધીને $2\,R$ થાય,તો પૃથ્વી દ્વારા મેળવાતી ઊર્જા પહેલા કરતાં કેટલા ગણી થાય?View Solution
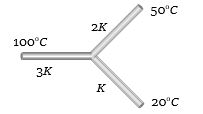
- 3સમાન લંબાઇ અને આડછેદ ધરાવતા સળિયા નીચે દર્શાવેલ મુજબના તાપમાને છે તો જંકશનનું તાપમાન ....... $^oC$ હશે?View Solution
- 4View Solutionજો સૂર્યનું (કાળો પદાર્થ) તાપમાન બમણું થાય, તો પૃથ્વી દ્વારા મેળવાતી ઊર્જા વધીને કેટલા ગણી થાય?
- 5બે સળિયાઓની લંબાઇ એકસમાન અને જુદી-જુદી વિશિષ્ટ ઉષ્માઓ $({S_1} , {S_2})$, ઉષ્માવાહકતા $\left(K_{1}, K_{2}\right)$ તથા આડછેદના ક્ષેત્રફળ $\left(A_{1}, A_{2}\right)$ અને બંનેના છેડાના તાપમાન $ {T_1} $ અને $ {T_2} $ છે. જો વહનને કારણે થતાં ઉષ્માના વ્યયનો દર સમાન હોય, તોView Solution
- 6$600\,K$ તાપમાને રહેલ ગોળાને $200\,K$ તાપમાનવાળા વાતાવરણમાં મુકેલ છે.તેનો ઠંડા પડવાનો દર $H$ છે.જો તેનું તાપમાન ઘટીને $400\,K$ થાય તો તેટલા જ વાતાવરણમાં તેનો ઠંડા પડવાનો દર કેટલો થાય?View Solution
- 7બે પદાર્થાે $A$ અને $B$ ને ઉષ્મીય ઉત્સર્જકતા અનુક્રમે $0.01$ અને $ 0.81$ છે. બંને પદાર્થની બહારનું ક્ષેત્રફળ સમાન છે. બંને પદાર્થે સમાન દરથી કુલ વિકિરણ પાવરનું ઉત્સર્જન કરે છે. .$\lambda_B$ તરંગલંબાઈએ $B$ દ્વારા મળતા મહત્તમ સ્પેક્ટ્રમ વિકિરણ $1.0 \mu m$ છે. જો $A$ નું તાપમાન $5802 K$ હોય તો,$B$ નું તાપમાન .... $K$View Solution
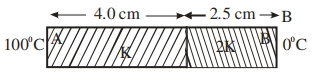
- 8આપેલ આકૃતિ અનુસાર, $K$ અને $2K$ જેટલી ઉષ્મીય વાહક્તા ધરાવતી બે તક્તિઓ $A$ અને $B$ ને એકસાથે જોડી એક સંયુક્ત તક્તિ બનાવવામાં આવે છે. તક્તિઓની જાડાઈ અનુક્રમે $4.0 \,cm$ અને $2.5 \,cm$ અને દરેેક તક્તિના આડછેદનું ક્ષેત્રફળ $120 \,cm ^{2}$ છે. સંયુક્ત તક્તિની સમતુલ્ય ઉષ્મીય વાહક્ત $\left(1+\frac{5}{\alpha}\right) K$ છે. તો $\alpha$ નું મૂલ્ય ............... થશે.View Solution
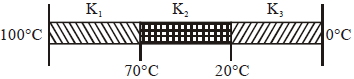
- 9ત્રણ સમાન આડછેદ અને લંબાઈ ધરાવતા સળિયાને જુદા-જુદા દ્રવ્યમાંથી બનાવેલ છે જેમની ઉષ્માવાહકતા અનુક્રમે $K _{1}, K _{2},$ અને $K _{3}$ છે. તેને પછી આકૃતિમાં દર્શાવ્યા પ્રમાણે જોડેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે સળિયાના એક છેડાને $100^{\circ} C$ તાપમાને અને બીજા છેડાને $0^{\circ} C$ તાપમાને રાખેલ છે જો સંતુલન સમયે સળીયાના જોડાણના જંકશનનું તાપમાન અનુક્રમે $70^{\circ} C$ અને $20^{\circ} C$ હોય અને સળિયાની સપાટી પરથી કોઈ પણ ઉર્જાનો વ્યય થતો ના હોય તો $K _{1}, K _{2}$ અને $K _{3}$ વચ્ચેનો સંબધ શું હશે?View Solution
- 10એક પદાર્થ $6$ મિનિટમાં $60^{\circ} C$ થી $40^{\circ} C$ સુધી ઠંડો પડે છે. જો પરિસરનું તાપમાન $10^{\circ} C$ હોય, તો પછીની $6$ મિનિટ પછી તેનું તાપમાન $.........{ }^{\circ} C$ થશે.View Solution
