Let height of tower be \(h\) and speed of projection in first two cases be \(u\).
For case-I : \(2^{\text {nd }}\) equation \(s=u t+\frac{1}{2}\) at \(^{2}\)
\(h =- u (6)+\frac{1}{2}\, g (6)^{2}\)
\(H =-6 u +18\,g \ldots\) \((i)\)
For case-II \(: h = u (1.5)+\frac{1}{2}\, g (1.5)^{2}\)
\(h =1.5 u +\frac{2.25 g }{2} \ldots\) \((ii)\)
Multiplying equation \((ii)\) by \(4\) we get
\(4 h =6 u +4.5\, g \ldots .\) \((iii)\)
equation \((i)\) \(+\) equation \((iii)\) we get \(5 h =22.5 g\)
\(h =4.5 g \ldots\) \((iv)\)
For case\(-III\)
\(h =0+\frac{1}{2} gt ^{2} \ldots\) \((v)\)
Using equation \((4)\)and equation \((5)\)
\(4.5 g=\frac{1}{2} g t^{2}\)
\(t ^{2}=9 \Rightarrow t =3 s\)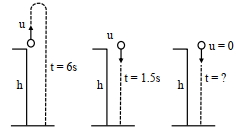
Download our appand get started for free
Similar Questions
- 1જમીનથી $h$ ઊંચાઈએથી એક દડાને શિરોલંબ રીતે નીચેની તરફ ફેંકવામાં આવે છે. તે જમીનને અથડાઇને ઉપરની દિશામાં ઉછળે છે. તેની અનુગામી ગતિ અને હવાના અવરોધને અવગણતા, નીચેનામાંથી કયો આલેખ ઝડપ $(v)$ અને ઊંચાઈ $(h)$ ના વક્રને ખરા અર્થમાં રજૂ કરે છે?View Solution
- 2એક બલૂન $29 \,ms^{-1}$ ના વેગથી ઉપર તરફ ગતિ કરે છે.તેમાંથી પથ્થર મૂકતાં તે $10 \,sec$ માં જમીન તે આવે છે તો બલૂન કેટલી ઊંચાઈએ ($m$ માં) હશે ત્યારે પથ્થર મુક્ત કરવામાં આવ્યો હશે?View Solution
($g = 9.8\,m/{s^2}$)
- 3કણ $X-$અક્ષ પર $x = 4(t - 2) + a{(t - 2)^2}$ મુજબ ગતિ કરે તો નીચેનામાંથી શું સાચું પડે?View Solution
- 4મકાનની ટોચ પરથી એક પથ્થરને મુક્ત કરવામાં આવે છે. જ્યારે આ પથ્થર ટોચથી $5\, m$ નીચે આપેલા બિંદુ પાસેથી પસાર થાય છે, ત્યારે ટોચથી $25\, m$ નીચે રહેલા બિંદુ પરથી બીજા પથ્થરને મુક્ત કરવામાં આવે છે. બંને પથ્થર મકાનનાં તળીયે એક સાથે પહોંચે છે. મકાનની ઊંચાઈ ($m$ માં) કેટલી હશે?View Solution
- 5નીચે બે કથન આપેલા છે.View Solution
કથન $I$ : વેગ-સમયના આલેખનું ક્ષેત્રફળ પદાર્થે આપેલ સમયમાં કાપેલું અંતર દર્શાવશે.
કથન $II$ : પ્રવેગ-સમયના આલેખનું ક્ષેત્રફળ બરાબર આપેલ સમયમાં વેગમાં થતો ફેરફાર હોય છે.
ઉપર્યુક્ત બંને કથનના સંદર્ભમાં, નીચે આપેલ વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 6એક બોલને $h$ ઊંચાઈએથી છોડવામાં આવે છે. જો $t_1$ અને $t_2$ અનુક્રમે અંતરના પ્રથમ અર્ધભાગ અને પછીના અર્ધભાગ માટેના સમય છે. તો $t_1$ અને $t_2$ વચ્ચેનો સાચો સંબંધ પસંદ કરો.View Solution
- 7એક બોલને $h$ ઊંચાઈએથી છોડવામાં આવે છે. જો $t_1$ અને $t_2$ અનુક્રમે અંતરના પ્રથમ અર્ધભાગ અને પછીના અર્ધભાગ માટેના સમય છે. તો $t_1$ અને $t_2$ વચ્ચેનો સાચો સંબંધ પસંદ કરો.View Solution
- 8View Solutionઅચળ પ્રવેગી ગતિ કરતાં કણ માટે સ્થાન, વેગ અને પ્રવેગનો આલેખ શેના વડે રજૂ કરવામાં આવે?
- 9બે પદાર્થો $A ($દળ $1 \ kg)$ અને $B ($દળ $3 \ kg)$ ને અનુક્રમે $16 m$ અને $25 m$ ની ઊંચાઇએથી છોડવામાં આવે છે. તેને જમીન પર પહોંચતાં લાગતા સમયનો ગુણોત્તર કેટલો થાય?View Solution
- 10પદાર્થ $r$ ત્રિજયા ના વર્તૂળ ના પરીઘ પર $A$ થી $B$ સુધી ગતી કરે, તો પથલંબાઈ અને સ્થાનાંતર કેટલા થાય?View Solution