$\text { M.S.R }=8.45 \mathrm{~cm}, V.C =26$
ચોસલામાંથી જોતાં પેપર પરના માર્ક (નિશાની) માટેનું અવોલક્ન$\text { M.S.R }=7.12 \mathrm{~cm}, V . C=41$
કાચની સપાટી ઉપરના પાવડર કણો માટેનું અવલોકન$\text { M.S.R }=4.05 \mathrm{~cm}, \mathrm{~V} . \mathrm{C}=1$
કાચના ચોસલાનો વક્કીભવનાંક. . . . .થશે.($M.S.R$. = મુખ્ય સ્કેલ પરનું અવલોકન$V.C$. = વર્નિંયર કેલીપર્સના કાપા)
$1 \mathrm{MSD}=\frac{1 \mathrm{~cm}}{20}=0.05 \mathrm{~cm}$
$1 \mathrm{VSD}=\frac{49}{50} \mathrm{MSD}=\frac{49}{50} \times 0.05 \mathrm{~cm}=0.049 \mathrm{~cm}$
$\mathrm{LC}=1 \mathrm{MSD}-1 \mathrm{VSD}=0.001 \mathrm{~cm}$
$\text { For mark on paper, } \mathrm{L}_1=8.45 \mathrm{~cm}+26 \times 0.001 \mathrm{~cm} $
$=84.76 \mathrm{~mm}$
$\text { For mark on paper through slab, } \mathrm{L} 2=7.12 \mathrm{~cm}+$
$41 \times 0.001 \mathrm{~cm}=71.61 \mathrm{~mm}$
$\text { For powder particle on top surface, } \mathrm{ZE}=4.05 \mathrm{~cm}$
$+1 \times 0.001 \mathrm{~cm}=40.51 \mathrm{~mm}$
$\therefore \text { actual } \mathrm{L}_1=84.76-40.51=44.25 \mathrm{~mm}$
$\quad \text { actual } \mathrm{L} 2=71.61-40.51=31.10 \mathrm{~mm}$
$\quad \mathrm{~L}_2=\frac{\mathrm{L}_1}{\mu}$
$\Rightarrow \mu=\frac{\mathrm{L}_1}{\mathrm{~L}_2}=\frac{44.25}{31.10}=1.42$
Download our appand get started for free
Similar Questions
- 1View Solutionચુંબકીય ચાકમાત્રાનો એકમ શું થાય?
- 2$M,L,T$ અને $C$ (કુલંબ) ના સ્વરૂપમાં ચુંબકીય ક્ષેત્રનું પારિમાણિક સૂત્ર શું થાય?View Solution
- 3ગોળાની ત્રિજ્યા $(7.50 \pm 0.85) \,cm $ માપવામાં આવે છે. ધારો કે તેના કદમાં પ્રતિશત ત્રુટિ $x$ છે. $x$ નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું ($\%$ માં) હશે?View Solution
- 4એક વિદ્યાર્થી સાદા લોલકના $100$ આવર્ત (દોલન) માટેનો સમય ચાર વખત માપે છે અને તે $90\;s$ ,$91\;s $,$95\;s$ અને $92\;s$ છે. જો ઘડિયાળની લઘુતમ માપશકિત $1\;s$ હોય, તો તેણે સરેરાશ સમય કેટલો લખવો જોઇએ?View Solution
- 5નીચે દર્શાવેલ ભૌતિક રાશિની કઇ જોડ માટે તેમનાં પારિમાણિક સૂત્રો સમાન છે?View Solution
$(1) $ ઊર્જા ઘનતા
$(2)$ વક્રીભવનાંક
$(3) $ ડાઇઇલેકટ્રિક અચળાંક
$(4) $ યંગ મોડયુલસ
$(5)$ ચુંબકીય ક્ષેત્ર
- 6View Solutionન્યુટન-સેકન્ડ એ શેનો એકમ છે?
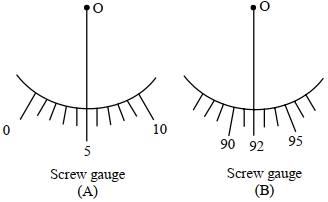
- 7વિદ્યાર્થી $A$ અને વિદ્યાર્થી $B$ સમાન પીચ ધરાવતા અને $100$ વર્તુળાકાર કાંપા ધરાવતા બે સ્ક્રૂગેજોનો ઉપયોગ આપેલ તારની ત્રિજ્યા માપવા માટે કરે છે. તારની ત્રિજ્યાનું સાચું મૂલ્ય $0.322\, {cm}$ છે. વિદ્યાર્થી $A$ અને $B$ દ્વારા વર્તુળાકાર સ્કેલના અવલોકનના તફાવતનું નિરપેક્ષ મૂલ્ય કેટલું હશે?View Solution
[જ્યારે સ્ક્રુ ગેજ બંધ હોય ત્યારે આકૃતિ $O$ સંદર્ભની સ્થિતિ દર્શાવે છે]
આપેલ : પીચ $=0.1 \,{cm}$.
- 8$ {G^x}{c^y}{h^z} $ નું પારિમાણીક સૂત્ર લંબાઇ જેવું છે.જયાં $G,c$ અને $h$ ગુરુત્વાકર્ષણ અચળાંક, પ્રકાશનો વેગ અને પ્લાન્કનો અચળાંક છે. તો નીચેનામાથી $x,y$ અને $z$ ના કયા મૂલ્યો સાચા છે.View Solution
- 9નીચે બે વિધાનો આપેલા છે. એકને કથન $A$ અને બીજાને કારણ $R$ થી દર્શાવવામાં આવ્યા છે.View Solution
ક્થન $(A)$ : પાણીના બુંદના દોલનોનો આવર્તકાળ પૃષ્ઠતાણ $(S)$ ઉપર આધાર રાખે છે, જો પ્રવાહીની ઘનતા $\rho$, બુંદની ત્રિજ્યા $r$ હોય, તો $T = K \sqrt{ \rho r ^3 / S ^{3 / 2}}$ એ પરિમાણિક રીતે સાચું છે. જ્યાં $K$ એ પરિમાણરહિત છે.
કારણ $(R)$ : પરિમાણીક વિશ્લેષણની મદદથી આપણાને જ.બા. સમય કરતા જુદું પરિમાણ મળે છે.
ઉપરોક્ત વિધાનોમાં સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી સાચો વિકલ્પ પસંદ કરો.
- 10View Solutionએકમ રહિત રાશિએ..... છે.
