Density of mercury, \(\rho_{1}=13.6 \times 10^{3} kg / m ^{3}\)
Height of the mercury column, \(h_{1}=0.76 m\)
Density of French wine, \(\rho_{2}=984 kg / m ^{3}\)
Height of the French wine column \(=h_{2}\)
Acceleration due to gravity, \(g=9.8 m / s ^{2}\)
The pressure in both the columns is equal, i.e.,
Pressure in the mercury column
\(=\) Pressure in the French wine column
\(\rho_{1} h_{1} g =\rho_{2} h_{2} g\)
\(h_{2}=\frac{\rho_{1} h_{1}}{\rho_{2}}\)
\(=\frac{13.6 \times 10^{3} \times 0.76}{984}\)
\(=10.5 m\)
Hence, the height of the French wine column for normal atmospheric pressure is \(10.5\; m\)
Download our appand get started for free
Similar Questions
- 1નીચે બે વિધાનો આપેલા છે. એકને કથન $A$ અને બીજાને કારણ $R$ થી દર્શાવવામાં આવ્યા છે.View Solution
ક્થન $(A)$ : જ્યારે તમે ટૂથપેસ્ટને બીજા છેડેથી બહાર કાઢવા માટે ટ્યુબના એક છેડાને દબાવો છો, ત્યારે પાસ્કલનો સિદ્ધાંત જોવા મળે છે.
કારણ $(R)$ : બંધ અદબનીય પ્રવાહી પર લાગુ પાડેલ દબાણમાં ફેરફાર પ્રવાહીના દરેક ભાગ અને તેના પાત્રની દિવાલો પર ઘટ્યા વગર પ્રસારિત થાય છે.
ઉપરોક્ત વિધાનોમાં સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી સાચો વિકલ્પ પસંદ કરો.
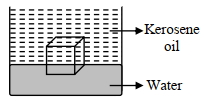
- 2એક બરફનો ચોસલો આંશિંક પાણીમાં અને આંશિક કેરોસીન તેલમાં તરે છે. પાણીમાં ડૂબાડેલ બરફના કદ અને કેરોસીન તેલમાંના બરફના કદનો ગુણોતર. . . . . . .છે (કેરોસીન તેલનુ) વિશિષ્ટ ગુરુત્વ = $0.8$ , બરફનું વિશિષ્ટ ગુરુત્વ =$0.9$) :View Solution
- 3$L,\frac{L}{2}$ અને $\frac{L}{3}$ લંબાઈની ત્રણ કેશળીઓ શ્રેણીમાં જોડેલ છે. તેમની ત્રિજ્યાઓ અનુક્કમે $r, \frac{r}{2}$ અને $\frac{r}{3}$ છે. પછી જો ધારારેખીય વહન જાળવી રાખવામાં આવે છે અને પહેલી કેશનળીની વચ્ચે દબાણ $P$ છે તો ...View Solution
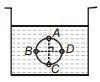
- 4આકૃતિમાં દર્શાવ્યા મુજબ $\rho$ ઘનતા ધરાવતા પ્રવાહીથી ભરેલું પાત્ર દર્શાવે છે. ચાર બિંદુુઓ $A, B, C$ અને $D$ એ આકૃતિમાં દર્શાવ્યા મુજબ વર્તુળના વિરુદ્ધ વ્યાસાં બિંદુુઓ પર છે. $A$ અને $C$ બિંદુઓ શિરોલંબ રેખા પર રહેલા છે અને $B$ અને $D$ બિંદુુઓ સમક્ષિતિજ રેખા પર રહેલા છે. ખોટું નિવેદન પસંદ કરો. ( $p_A,p_B, p_C, p_D$ એ અનુક્કમિત બિંદુઓ પરનું $A$ નિરપેક્ષ દબાણ છે.View Solution
- 5બહારની ત્રિજ્યા $R$ ધરાવતો એક પોલો ગોળો પાણીની સપાટીની અંદર માત્ર ડૂબેલો છે. પોલા ગોળાની અંદરની ત્રિજ્યા $r$ છે. જો ગોળાના દ્રવ્યની પાણીની સાપેક્ષે ઘનતા $\frac{27}{8}$ હોય તો $r$ નું મૂલ્ય $......R$ જેટલું હશે?View Solution
- 6વેન્યુરીમીટર $..........$ પર કાર્ય કરે છે.View Solution
- 7View Solutionશ્યાનતા ખેંચાણ બળ શેના પર આધાર રાખે છે?
- 8પાણીની અંદર $1\,cm$ ત્રિજ્યાના હવાના પરપોટાનો ઉપરની દિશામાંનો પ્રવેગ $9.8\, cm\, s ^{-2}$ છે. પાણીની ઘનતા $1\, gm\, cm ^{-3}$ અને પાણી દ્વારા પરપોટા પર નહિવત ઘર્ષણબળ લાગે છે. તો પરપોટાનું દળ $.......gm$ હશે.View Solution
$\left( g =980 \,cm / s ^{2}\right)$
- 9View Solutionવિધાન : પ્રવાહમાં જ્યારે દબાણ વધુ હોય ત્યાં વેગ ઓછો હોય અને ઊલટું પણ (દબાણ ઓછું અને વેગ વધુ)
કારણ : બર્નુલીના નિયમ મુજબ આદર્શ પ્રવાહીના વહન માટે એકમ દળમાં રહેલ કુલ ઉર્જા અચળ હોય.
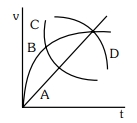
- 10એક ગોળાકાર બોલને ખુબજ સ્નિગ્ધ પ્રવાહીના લાંબા સ્તંભમાં મુક્ત (છોડવામાં)કરવામાં આવે છે.આકૃતિમાં દર્શાવેલ વક્ર,કે જે બોલ માટે ઝડપ $(v)$ અને સમય $(t)$ના વિધેય તરીકે દર્શાવે તે$........$છે.View Solution