ત્રણ $4\,\Omega ,6\,\Omega $ અને $12\,\Omega $ ના અવરોધો સમાંતર માં જોડેલા છે અને આ તંત્ર ને $1\,\Omega $ આંતરિક અવરોધ અને $1.5\, V$ ની બેટરી સાથે શ્રેણીમાં જોડેલ છે. $4\,\Omega $ ના અવરોધ માંથી ઉત્પન્ન થતી જૂલ ઉષ્માનો દર કેટલા ................. $W$ હશે?
AIEEE 2012, Diffcult
c
Resistors \(4\, \Omega, 6\, \Omega\) and \(12 \,\Omega\) are connected in parallel, its equivalent resistance \((R)\) is given by
Resistors \(4\, \Omega, 6\, \Omega\) and \(12 \,\Omega\) are connected in parallel, its equivalent resistance \((R)\) is given by
\(\frac{1}{R}=\frac{1}{4}+\frac{1}{6}+\frac{1}{12} \Rightarrow R=\frac{12}{6}=2 \,\Omega\)
Again \(R\) is connectedto \(1.5 \,\mathrm{V}\) battery whose internal resistance \(r=1\, \Omega\)
Equivalent resistance now, \(R^{\prime}=2\, \Omega+1 \,\Omega=3\, \Omega\)
Current, \(I_{\text {total }}=\frac{V}{R^{\prime}}=\frac{1.5}{3}=\frac{1}{2} \,\mathrm{A}\)
\(I_{\text {total }}=\frac{1}{2}=3 x+2 x+x=6 x\)
\(\Rightarrow x=\frac{1}{12}\)
\(\therefore \) Current through \(4\, \Omega\) resistor \(=3 x\)
\(=3 \times \frac{1}{12}=\frac{1}{4}\, A\)
Therefore, rate of Joule heating in the \(4 \,\Omega\) resistor
\(=I^{2} R=\left(\frac{1}{4}\right)^{2} \times 4=\frac{1}{4}=0.25 \,\mathrm{W}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
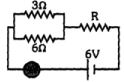
- 1જો આપેલ આકૃતિમાં એમિટર $2\,A$ નું માપન દર્શાવે તો $R$ શોધો............. $\Omega$View Solution
- 2વોલ્ટમીટરના માપાંકન(calibration) માં એક $ 1.1\,volt\,\, e.m.f$ ધરાવતા કોષને $440\,cm$ લંબાઈના તાર વહે સંતુલિત કરેલ છે. અવરોધ વચ્ચેનો વિદ્યુતસ્થિતિમાનનો તફાવત $220\,cm$ લંબાઈના તાર દ્વારા સંતુલિત થયેલ છે. તેને અનુરૂપ વોલ્ટમીટરનું અવલોકન $0.5\,volt$ મળે છે તો વોલ્ટમીટરના માપનમા કેટલા ................ $volt$ ત્રુટિ આવે?View Solution
- 3જ્યારે અવરોધમાંથી $2\, A$ પ્રવાહ પસાર થાય છે ત્યારે તે $15\, s$, માં $300 \,J$ ઉષ્મા ઉર્જા ઉત્પન્ન કરે છે. જો પ્રવાહ વધારીને $3\, A$ કરવામાં આવે છે તો $10 s$ માં ઉત્પન્ન ઊર્જા........$J$ થશે.View Solution
- 4પ્રવાહ પસાર થતાં વાહકનું તાપમાન $5\,^oC$ વધે છે. જ્યારે પ્રવાહ બમણો કરવામાં આવે ત્યારે તો તેમાં તાપમાનનો કેટલા $^oC$ નો વધારો થાય?View Solution
- 5આપેલ નળાકાર તારની લંબાઈ $100\,\%$ જેટલી વધેલી છે. વ્યાસમાં થતાં સતત ઘટાડાને લીધે તારના અવરોધમાં થતો ફેરફાર ................ $\%$ હશે.View Solution
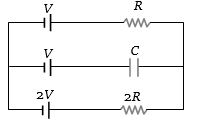
- 6View Solutionઆપેલ પરિપથમાં કેપેસિટર વચ્ચેનો વોલ્ટેજ કેટલો થાય?
- 7જો તાંબાના તારને તેની લંબાઈમાં $20\%$ વધારો મેળવવા માટે ખેંચવામાં આવે તો તેના અવરોધમાં $.............\%$ વધારો થાય.View Solution
- 8કોઇ અવરોધ $R$ માંથી પસાર થતો વિદ્યુતભાર, સમય $t $ સાથે $ Q=at-bt^2 $ અનુસાર બદલાય છે.જયાં $a $ અને $b$ ઘન અચળાંકો છે. $R$ માં ઊત્પન્ન થતી કુલ ઉષ્મા કેટલી હશે?View Solution
- 9$12\, ohm$ અવરોધ ધરાવતા તારને વાળીને સમબાજુ ત્રિકોણ બનાવવામાં આવે તો બે ખૂણા વચ્ચેનો સમતુલ્ય અવરોધ કેટલો થાય?View Solution
- 10એક વિધુત કિટલીમાં બે ફિલામેન્ટ છે. તે પૈકીનો પ્રથમ ફિલામેન્ટ અમુક પાણીને $10$ મિનિટમાં ઉકળતું કરે છે અને બીજો ફિલામેન્ટ તેને $15$ મિનિટમાં ઉકળતું કરે છે. બંને ફિલામેન્ટને સમાંતર જોડાતાં હવે આ પાણી .............. મિનિટમાં ઉકળવા લાગશે.View Solution
