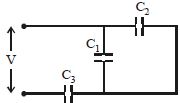
Equivalent capacitance of circuit,
\(\frac{1}{C_{e q}}=\frac{1}{C_{3}}+\frac{1}{C_{1}+C_{2}}\)
(since \(\mathrm{C}_{1}\) and \(\mathrm{C}_{2}\) are in parallel and which is in series with \({\mathrm{C}}_{3}\) ).
ie, \(\frac{1}{\mathrm{C}_{\mathrm{eq}}}=\frac{\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3}}{\mathrm{C}_{3}\left(\mathrm{C}_{1}+\mathrm{C}_{2}\right)}\)
\(\therefore C_{e q}=\frac{C_{3}\left(C_{1}+C_{2}\right)}{C_{1}+C_{2}+C_{3}}\)
since \(V\) is the voltage of battery, charge, \(\mathrm{q}=\mathrm{C}_{\mathrm{eq}} \mathrm{V}\)
\(=\frac{\mathrm{C}_{3}\left(\mathrm{C}_{1}+\mathrm{C}_{2}\right) \mathrm{V}}{\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3}}\)
If the capacitor \(\mathrm{C}_{3}\) breaks down, then effective capacitance, \(C_{e q}^{\prime}=C_{1}+C_{2}\)
New charge \(q'=\) \(\mathrm{C}_{\mathrm{eq}}^{\prime} \mathrm{V}=\left(\mathrm{C}_{1}+\mathrm{C}_{2}\right) \mathrm{V}\)
Change in total charge \(=q^{\prime}-q\)
\(=\left(\mathrm{C}_{1}+\mathrm{C}_{2}\right) \mathrm{V}-\frac{\mathrm{C}_{3}\left(\mathrm{C}_{1}+\mathrm{C}_{2}\right) \mathrm{V}}{\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3}}\)
\(=\left(\mathrm{C}_{1}+\mathrm{C}_{2}\right) \mathrm{V}\left[1-\frac{\mathrm{C}_{3}}{\mathrm{C}_{1}+\mathrm{C}_{2}+\mathrm{C}_{3}}\right]\)
Download our appand get started for free
Similar Questions
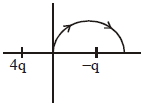
- 1$x-$અક્ષ પર $4 q$ અને $-q$ વિજભાર ધરાવતા બે બિંદુવત વિજભાર $x=-\frac{d}{2}$ અને $x=\frac{d}{2}$ સ્થાને જડેલ છે. જો ત્રીજા $'q'$ જેટલા બિંદુવત વિજભારને આકૃતિમાં દર્શાવ્યા પ્રમાણે ઉગમબિંદુથી $x = d$ સુધી અર્ધવર્તુળાકાર માર્ગ પર લઈ જવામાં આવે છે. તો તે દરમિયાન વિજભારની ઉર્જા....View Solution
- 2બે પ્લેટો પરનો વિદ્યુતસ્થિતિમાન અનુક્રમે $-10\, V$ અને $+ 30 \,V$ બે પ્લેટો વચ્ચેનું અંતર $2\, cm$ હોય તો તેમની વચ્ચેનું વિદ્યુત ક્ષેત્ર....$V/m$View Solution
- 3View Solutionડાઇઇલેકિટ્રક ભરેલાં કેપેસિટરને બેટરી સાથે જોડેલ છે.હવે બેટરી દૂર કરીને ડાઇઇલેકિટ્રકને બહાર કાઢતા કેપેસિટરના વિદ્યુતસ્થિતિમાન વિરુધ્ધ બહાર નીકળેલ ડાઇઇલેકિટ્રકની લંબાઇનો આલેખ કેવો થાય?
- 4$27$ એક સમાન બુંદોને દરેકને $22 \,V$ થી વિદ્યુત ભારીત કરવામાં આવે છે. તેઓ સંયોજાઈને એક મોટું બુંદ બનાવે છે. મોટાં બુંદનું સ્થિતિમાન.......$V$ થશે.View Solution
- 5દસ વિદ્યુતભારને $R$ ત્રિજ્યાના વર્તુળ પર સમાન કોણીય અંતરે મૂકેલા છે. વિધુતભાર $1,3,5,7,9$ પાસે $(+q)$ અને વિધુતભાર $2,4,6,8,10$ પાસે $(-q)$ વિધુતભાર છે તો વર્તુળના કેન્દ્ર આગળ વિદ્યુતક્ષેત્ર અને વિદ્યુતસ્થિતિમાનView Solution
- 6સમાંતર પ્લેટ કેપેસીટરનું કેપેસીટન્સ $12\ \mu F$ છે જો પ્લેટો વચ્ચેનું અંતર બમણુ તથા ક્ષેત્રફળ અડધુ કરવામાં આવે તો નવું કેપેસીટન્સ...$\mu F$View Solution
- 7અવકાશમાંનાં અમુક વિસ્તારમાં, ઉગમબિંદુથી $x$ - અક્ષની સાપેક્ષે ગતિ કરતાં મળતાં વિદ્યુતક્ષેત્રનું ચલન દર્શાવવા $V=8 x^2+2$ વાપરવામાં આવે છે. અહી $x$ એ કોઈપણ બિંદુનો $x$ યામ છે .આ રીતે બિંદુ $(-4,0)$ પર વિદ્યુતક્ષેત્રનું મૂલ્ય .......... $V / m$ મળશે.View Solution
- 8આકૃતિમાં દર્શાવ્યા અનુસાર વિદ્યુતભાર $Q$ એ $L$ લંબાઇના સળિયા $AB$ પર સમાન રીતે પથરાયેલ છે.સળિથાના છેડા $A$ થી $L$ અંતરે રહેલા બિંદુ આગળ વિદ્યુતવિભવ ( વિદ્યુતસ્થિતિમાન ) ______ છે.View Solution

- 9સમબાજુ ત્રિકોણનાં શિરોબિંદુ પર $2 q,-q$ અને $-q$ મૂકવામાં આવે છે, ત્રિકોણનાં કેન્દ્ર પરView Solution
- 10નીચેની આકૃતિમાં સમસ્થિતિમાન વિસ્તાર દર્શાવેલ છે. આકૃતિમાં ઘન વીજભારને $A$ થી $B$ લઇ જવા માટે ...View Solution