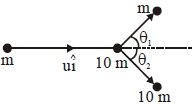
By momentum conservation along \(y\)
\(m _{1} u _{1} \sin \theta_{1}= m _{2} u _{2} \sin \theta_{2}\)
i.e. \(mu _{1} \sin \theta_{1}=10 mu _{2} \sin \theta_{2}\)
\(\Rightarrow u _{1} \sin \theta_{1}=10 u _{2} \sin \theta_{2}\) \(...(i)\)
\(kf _{ m _{ 1 }}=\frac{1}{2} ki _{ m _{ 1 }}\) i.e. \(\frac{1}{2} mu _{1}^{2}=\frac{1}{2} \times \frac{1}{2} mu ^{2}\)
i.e. \(\sqrt{ u _{1}=\frac{ u }{\sqrt{2}}}\) \(...(ii)\)
Also collision is elastic : \(k _{ i }= k _{ f }\)
\(\frac{1}{2} m u^{2}=\frac{1}{2} m u_{1}^{2}+\frac{1}{2} \cdot 10 m \cdot u_{2}^{2}\)
\(\frac{1}{2} mu ^{2}=\frac{1}{2} \times \frac{1}{2} mu ^{2}+\frac{1}{2} \times 10 m \cdot u _{2}^{2}\)
\(\frac{1}{4} mu ^{2}=\frac{1}{2} \times 10 \times mu _{2}^{2}\)
\(u _{2}=\frac{ u }{\sqrt{20}}\)\(...(iii)\)
Putting \((ii)\) \(\&\) \((iii)\) in \((i)\)
\(\frac{ u }{\sqrt{2}} \sin \theta_{1}=10 \cdot \frac{ u }{\sqrt{20}} \sin \theta_{2}\)
\(\sin \theta_{1}=\sqrt{10} \sin \theta_{2} \quad \rightarrow\) Hence \(n =10\)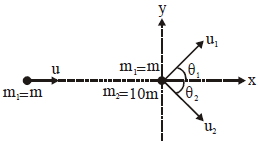
Download our appand get started for free
Similar Questions
- 1$20 \,g$ દળની ગોળી $100 \,m / s$ પ્રારંભિક ઝડપથી રાઈફલમાંથી છૂટે છે અને એજ સ્તરે રહેલા લક્ષ્ય પર $50 \,m / s$ ઝડપથી લક્ષ્યને અથડાય છે. હવાનાં અવરોધ વડે થયેલ કાર્યની માત્રા ........ $J$ હશે.View Solution
- 2$u\hat i$ શરૂઆતનો વેગ ધરાવતો એક $m$ દળનો પદાર્થ એક $3m$ દળના સ્થિર પડેલા પદાર્થ સાથે સંપૂર્ણ સ્થિતિસ્થાપક સંઘાત અનુભવે છે. તે સંઘાત પછી $v\hat j$ જેટલા વેગથી ગતિ કરે તો વેગ $v$ કેટલો હશે?View Solution
- 3પદાર્થ $5\;N$ ના બળની અસર હેઠળ સીધી રેખામાં $10\;m$ સ્થાનાંતર કરે છે. જો $25\; J$ કાર્ય થાય , તો બળે ગતિની દિશા સાથે કેટલો ખૂણો ($^o$ માં) બનાવ્યો હશે?View Solution
- 4જો ડેમમાથી પાણી $19.6\, m$ નીચે ટર્બાઇન વ્હીલ પર પડતું હોય તો ટર્બાઇન પાસે પાણીનો વેગ કેટલા ......... $\mathrm{m} / \mathrm{s}$ હશે? ($g = 9.8\, m/s^2$)View Solution
- 5$100\,kW$ ટ્રાન્સમીટર દ્વારા એક કલાક્માં આદર્શ સ્થિતિમાં વિખેરીત થતી ઊર્જા$......$હશે.View Solution
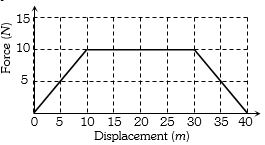
- 6કણનો બળ વિરુધ્ધ સ્થાનનો આલેખ આપેલ છે.તો $ x = 0 m$ થી $x = 35 m $ સુધીમાં કેટલા .......... $J$ કાર્ય થશે?View Solution
- 7બે પદાર્થો $16:9$ ના ગુણોત્તરમાં ગતિઊર્જા ધરાવે છે.જો તેઓને સમાન રેખીય વેગમાન હોય તો તેમના દળોનો ગુણોત્તર ........ થશે.View Solution
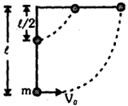
- 8$L$ લંબાઈના એક હલકા સળિયાને ઉપરના છેડાની શરૂઆતમાં મુકેલો છે. બે દળો (દરેકનું $m $ દળ) સળિયા સાથે જોડાયેલા છે. જેમાં એક સળિયાના મધ્યબિંદુએ અને બીજો દળ મુક્ત છેડે છે. નીચેના દળના છેડા આગળ કેટલો સમક્ષિતિજ વેગ લાગુ પાડવો જોઈએ કે જેથી સળિયો સમક્ષિતિજ રીતે રહે.View Solution
- 9સ્થિર સ્થિતિમાં રહેલ $m$ દળના પદાર્થ પર અચળ બળ લાગવાના કારણે તે $d$ જેટલું અંતર કાપીને પ્રાપ્ત કરેલી ગતિઊર્જા $K$ કોના સમપ્રમાણમાં હશે?View Solution
- 10View Solutionખોટું વિંધાન પસંદ કરો
