Electric flux density
\((\vec{D})=\frac{\text { charge }}{\text { Area }} \times \hat{r}=\frac{Q}{4 \pi r^{2}} \hat{r}=\epsilon_{0}\left(\frac{Q}{4 \pi \epsilon_{0} r^{2}} \hat{r}\right)\)
\(\Rightarrow \vec{E}=\frac{\vec{D}}{\epsilon_{0}}=\frac{e^{-x} \sin y \hat{i}-e^{-x} \cos y \hat{j}+2 z \hat{k}}{\epsilon_{0}}\)
Also by Gauss's law
\(\frac{\rho}{\epsilon_{0}}=\left(\frac{\partial}{\partial x} \hat{i}+\frac{\partial}{\partial y} \hat{j}+\frac{\partial}{\partial z} \hat{k}\right) \cdot \vec{E}=\left(\frac{\partial}{\partial x} \hat{i}+\frac{\partial}{\partial y} \hat{j}+\frac{\partial}{\partial z} \hat{k}\right) \cdot \frac{\vec{D}}{\epsilon_{0}}\)
\(\Rightarrow \rho=\frac{\partial}{\partial x}\left(e^{-x} \sin y\right)+\frac{\partial}{\partial y}\left(-e^{-x} \cos y\right)+\frac{\partial}{\partial z}(2 z)\)
\(\rho=-e^{-x} \sin y+e^{-x} \sin y+2\)
At origin \(\rho=-e^{-0} \sin 0+e^{-0} \sin 0+2\)
\(\rho=2 {C} / {m}^{3}\)
Charge \(=\rho \times\) volume \(=2 \times 2 \times 10^{-9}=4 \times 10^{-9}=4 {nC}\)
Download our appand get started for free
Similar Questions
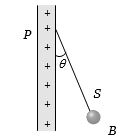
- 1આકૃતીમાં દર્શાવ્યા મુજબ મોટી વિદ્યુતભારીત પ્લેટ $P$ સાથે બાંધેલી દોરી $S$ બે બોલ $B$ ને ખૂણો બને તે રીતે લટકાવેલ છે તો પ્લેટની વિદ્યુતભારની પૃષ્ઠ ઘનતા કોના સમપ્રમાણમાં છે?View Solution
- 2$q_1$ બિંદુવત વિદ્યુતભાર $q_2$ વિદ્યુતભાર પર $F$ બળ લાગુ પાડે છે. જો બીજો એક વિદ્યુતભાર $q_3$ ને $q_2$ વિદ્યુતભારની એકદમ નજીક મૂકવામાં આવે તો $q_1$ વિદ્યુતભાર દ્વારા $q_2$ વિદ્યુતભાર પર લાગતું બળ કેટલું હશે ?View Solution
- 3$l$ લંબાઇની રેખા પર $q$, $Q$ અને $4q$ વિદ્યુતભારને એક છેડાથી અનુક્રમે $0,\,\frac {l}{2}$ અને $l$ અંતરે મૂકેલા છે. જો વિજભાર $q$ પર લાગતું બળ શૂન્ય કરવું હોય તો $Q$ વિજભાર કેટલો હોવો જોઈએ?View Solution
- 4$Y$ અક્ષ પર $10^3 \,V/m$ ની સમાન વિદ્યુતક્ષેત્રની ક્ષમતા વિતરણ પામેલી છે. $1\, g$ દળ અને $10^{-6} \,C$ વિદ્યુતભાર વાળો એક પદાર્થ ધન $x$ -અક્ષની દિશામાં ઉગમબિંદુથી ક્ષેત્રમાં $10\,m/s$ ના વેગથી પ્રક્ષેપણ કરે છે. $10\ s$ પછી તેની ઝડપ $m/s$ માં ........ છે.View Solution
- 5View Solutionજ્યારે સુવાહક સાબુના ફિણને ઋણભારીત કરવામાં આવે તો
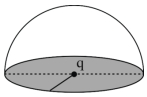
- 6જો વિંદ્યુતભાર $q$ ને અવાહક સપાટી ધરાવતા બંધ અર્ધગોળાકારનાં કેન્દ્ર આગળ મૂકવામાં આવે તો સપાટ સપાટીમાંથી પસાર થતું ફુલ ફ્લક્સ ............ થશે.View Solution
- 7ઉગમબિંદુ પર કેન્દ્ર રહે તેમ વિધુતડાઇપોલ $X$- અક્ષ પર મુકેલ છે. $OP$ રેખા $x$-અક્ષ સાથે $\theta$ ખૂણો બનાવે છે.જો $P$ બિદું આગળ વિધુતક્ષેત્ર $y$- અક્ષની દિશામા હોય તો $\theta$ નું મૂલ્ય કેટલું થાય?View Solution
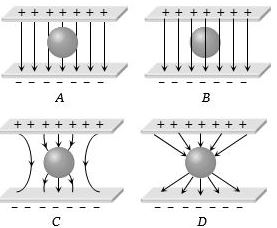
- 8View Solutionધાતુના ગોળાને વિદ્યુતક્ષેત્રમાં મૂકતાં વિદ્યુતક્ષેત્ર રેખા કેવી દેખાય?
- 9$R$ ત્રિજ્યા વાળી એક સમાન રીતે વિદ્યુતભારિત થયેલી રિંગની અક્ષ પર લાગતું વિદ્યુતક્ષેત્રનું મહત્તમ મૂલ્ય તેના કેન્દ્રથી $h$ અંતર આગળ છે. $h$ નું મૂલ્ય હશે.View Solution
- 10આપેલ વિસ્તારમાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=\left(\frac{3}{5} E _{0} \hat{i}+\frac{4}{5} E _{0} \hat{j}\right) \frac{ N }{ C }$ વડે આપવામાં આવે છે. $(y-z$ સમતલને સમાંતર) $0.2 \,m^ 2$ ક્ષેત્રફળ ધરાવતી અને $(x-y$ સમતલને સમાંતર) $0.3 \,m^2$ ક્ષેત્રફળ ધરાવતી લંબચોરસ સપાટીમાંથી બતાવેલ ક્ષેત્ર પસાર થતાં મળતા ફ્લક્સનો ગુણોત્તર $a:b$ છે, જ્યાં $a=...........$ છે.View Solution
[ અત્રે $\hat{i}, \hat{j}$ અને $\hat{k}$ એ અનુક્રમે $x, y$ અને $z-$ અક્ષોની દિશામાં એકમ સદિશ છે.]
