આપેલ વિસ્તારમાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=\left(\frac{3}{5} E _{0} \hat{i}+\frac{4}{5} E _{0} \hat{j}\right) \frac{ N }{ C }$ વડે આપવામાં આવે છે. $(y-z$ સમતલને સમાંતર) $0.2 \,m^ 2$ ક્ષેત્રફળ ધરાવતી અને $(x-y$ સમતલને સમાંતર) $0.3 \,m^2$ ક્ષેત્રફળ ધરાવતી લંબચોરસ સપાટીમાંથી બતાવેલ ક્ષેત્ર પસાર થતાં મળતા ફ્લક્સનો ગુણોત્તર $a:b$ છે, જ્યાં $a=...........$ છે.
[ અત્રે $\hat{i}, \hat{j}$ અને $\hat{k}$ એ અનુક્રમે $x, y$ અને $z-$ અક્ષોની દિશામાં એકમ સદિશ છે.]
JEE MAIN 2021, Diffcult
d
\(\overrightarrow{ E }=\left(\frac{3 E _{0}}{5} \hat{ i }+\frac{4 E _{0}}{5} \hat{ j }\right) \frac{ N }{ C }\)
\(\overrightarrow{ E }=\left(\frac{3 E _{0}}{5} \hat{ i }+\frac{4 E _{0}}{5} \hat{ j }\right) \frac{ N }{ C }\)
\(A_{1}=0.2 m ^{2}\) [parallel to \(y - z\) plane \(]\)
\(=\overrightarrow{ A }_{1}=0.2 m ^{2} \hat{ i }\)
\(A_{2}=0.3 m ^{2}\) [parallel to \(x - z\) plane \(]\)
\(\overrightarrow{ A }_{2}=0.3 m ^{2} \hat{ j }\)
Now \(\phi_{a}=\left[\frac{3 E_{0}}{5} \hat{i}+\frac{4 E_{0}}{5} \hat{j}\right] \cdot[0.2 \hat{i}]=\frac{3 \times 0.2}{5} E _{0}\)
\( \phi_{b}=\left[\frac{3 E_{0}}{5} \hat{i}+\frac{4 E_{0}}{5} \hat{j}\right] \cdot[0.3 \hat{j}]=\frac{4 \times 0.3}{5} E _{0}\)
\(\operatorname{Now} \frac{\phi_{ a }}{\phi_{ b }}=\frac{0.6}{1.2}=\frac{1}{2}=\frac{ a }{ b }\)
\(\Rightarrow a: b=1: 2\)
\(\Rightarrow a=1\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$+\sigma_{\mathrm{s}} \mathrm{C} / \mathrm{m}^2$ જેટલી નિયમિત પૃષ્ઠ વિદ્યુતભાર ધનતા ધરાવતી એક અનંત સમતલ તક્તિને $x-y$ સમતલમાં મૂકવામાં આવે છે. બીજા એક $+\lambda_{\mathrm{e}} \mathrm{C} / \mathrm{m}$ જેટલી નિયમિત રેખીય વિધુતભાર ધનતા ધરાવતા અનંત લંબાઈના લાંબા તાર ને $z=4 \mathrm{~m}$ સમતલ અને $y$-અક્ષને સમાંતર રાખવામાં આવે છે. જો મૂલ્યોમાં $\left|\sigma_s\right|=2\left|\lambda_{\mathrm{e}}\right|$ હોય તો $(0,0,2)$ સ્થાન આગળ તક્તિ ( પૃષ્ઠ) વિદ્યુતભાર અને રેખીય વિધુત ભાર ને કારણે મળતા વિધુતક્ષેત્રનાં મૂલ્યોનો ગુણોતર. . . . . છે.View Solution
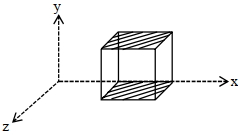
- 2એક સમઘનને $\overrightarrow{{E}}=150\, {y}^{2}\, \hat{{j}}$ જેટલા વિદ્યુતક્ષેત્રની અંદર મૂકવામાં આવે છે. સમઘનની બાજુની લંબાઈ $0.5 \,{m}$ અને તેને આકૃતિમાં દર્શાવ્યા પ્રમાણે મૂકવામાં આવે છે. સમઘનની અંદરનો વિદ્યુતભાર $(\times 10^{-11} {C}$ માં) કેટલો હશે?View Solution
- 3$a$ બાજુવાળા સમબાજુ ત્રિકોણના શિરોબંદુ પર $+Q$ વિદ્યુતભાર મૂકેલા છે.તો એક વિદ્યુતભાર પર લાગતું બળ કેટલું થાય? $\left( {k = \frac{1}{{4\pi {\varepsilon _0}}}} \right)$View Solution
- 4બે સમાંતર સુવાહક પૃષ્ઠોની એકબાજુનું ક્ષેત્રફળ $A$ છે. જો કોઈ એક પૃષ્ઠને વિદ્યુતભાર $Q$ આપવામાં આવે અને બીજીને તટસ્થ રાખવામાં આવે, તો બંને પૃષ્ઠોની વચ્ચે કોઈ બિંદુ પાસે વિદ્યુતક્ષેત્ર કેટલું છે ?View Solution
- 5બે બિંદુવત વિદ્યુતભારો વચ્ચેનું અપાકર્ષી બળ $F$ હોય ત્યારે તેમની વચ્ચેનું અંતર $1\, m$ છે. હવે આ બિંદુવત વિદ્યુતભારને $25\, cm$ ની ત્રિજ્યાવાળા ગોળા પરના વિદ્યુતભાર વડે બદલવામાં આવે છે. તેઓના કેન્દ્રો વચ્ચે અંતર $1 \,m$ છે. તો બે કિસ્સાઓમાં અપાકર્ષી બળ......મુજબ ઘટશે.View Solution
- 6$R$ ત્રિજ્યા ધરાવતા એક ગોલીય કવચ પર નિયમિત પૃષ્ઠ વીજભાર ઘનતા $\sigma$ છે. ગોલીય કવચની સપાટી ઉપર કોઈ પણ બિંદુ આગળ વિદ્યુતક્ષેત્ર. . . . . થશે.View Solution
- 7$10\,cm$ બાજુવાળા સમબાજુ ત્રિકોણ $ABC$ ના શિરોબિંદુ પર અનુક્રમે $1\,\mu C$ , $-1\,\mu C$ અને $2\,\mu C$ વિદ્યુતભાર મૂકતાં $C$ પર રહેલ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 8બે વિદ્યુતભાર $(+Q)$ અને $(-2Q)$ ઉદ્ગમબિંદુથી $X$ - અક્ષ પર અનુક્રમે $a$ અને $2a$ અંતરે મૂકેલ છે, તો વિદ્યુતક્ષેત્ર કયા અંતરે શૂન્ય થાય?View Solution
- 9$R$ ત્રિજયાના ગોળાના કેન્દ્રથી અંતર નો વિદ્યુતક્ષેત્ર $E$ વિરુધ્ધનો આલેખ કેવો થાય?View Solution
- 10$a$ ત્રિજ્યા અને રેખીય વિદ્યુતભાર ઘનતા $\lambda$ વાળા એક અર્ધ વર્તૂળના કેન્દ્ર $O$ આગળ વિદ્યુતક્ષેત્ર શેના દ્વારા આપી શકાય છે?View Solution