$u\hat i$ શરૂઆતનો વેગ ધરાવતો એક $m$ દળનો પદાર્થ એક $3m$ દળના સ્થિર પડેલા પદાર્થ સાથે સંપૂર્ણ સ્થિતિસ્થાપક સંઘાત અનુભવે છે. તે સંઘાત પછી $v\hat j$ જેટલા વેગથી ગતિ કરે તો વેગ $v$ કેટલો હશે?
JEE MAIN 2020, Diffcult
d
From momentum conservation
From momentum conservation
\(\overrightarrow{ P }_{ i }=\overrightarrow{ P }_{ f }\)
\(m ( ui )+3 m ( D )= mvj +3 m \overline{ v }_{2}\)
\(mui - mvj =3 m \overline{ v }_{1}\)
\(\bar{v}_{1}=\frac{u i-v j}{3}\)
or \(\left| v _{1}\right|=\frac{\sqrt{ u ^{2}+ v ^{2}}}{3}\)
or \(v_{1}^{2}=\frac{u^{2}+v^{2}}{9} \ldots .(1)\)
As collision is perfectely elastic hence
\(k_{i}=k_{j}\)
\(\frac{1}{2} m u^{2}+\frac{1}{2} 3 m 0^{2}=\frac{1}{2} m v^{2}+\frac{1}{2} 3 m v_{1}^{2}\)
\(\Rightarrow u ^{2}= v ^{2}+3 v _{1}^{2}\)
\(u ^{2}= v ^{2}+3 \frac{\left( u ^{2}+ v ^{2}\right)}{9}\)
\(\Rightarrow 3 u ^{2}=3 v ^{2}+ u ^{2}+ v ^{2}\)
\(\Rightarrow 2 u ^{2}=4 v ^{2}\)
\(v =\frac{ u }{\sqrt{2}}\)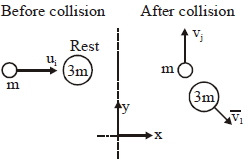
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$m$ દળ ધરાવતા પથ્થરને, દોરી વડે બાંધી, નિયમિત ઝડપ સાથે શિરોલંબ વર્તુળમાં ફેરવવામાં આવે છે. દોરીમાં તણાવ...View Solution
- 2View Solutionજ્યારે એક પદાર્થ અચળ ઝડપથી વર્તુળ પર ગતિ કરે, ત્યારે .......
- 3$0.5 \,kgs ^{-1}$ ના વેગથી ગતિ કરતા કન્વેયર બેલ્ટ પરથી સ્થિર ડ્રોપર વડે $5 \,ms ^{-1}$ ના દરથી ધૂળને પડવા દેવામાં આવે છે. બેલ્ટને ફરતી રાખવા માટે જરૂરી કાર્યત્વરા (પાવર) .......... $W$ થશે.View Solution
- 4$1.67 \times {10^{ - 27}}kg$ દળ ધરાવતો એક ન્યૂટ્રોન ${10^8}m/s$ વેગથી ગતિ કરીને સ્થિર ડ્યુટેરોન સાથેના સંઘાત બાદ તેની સાથે ચોંટી જાય છે. જો ડ્યુટેરોન નું દળ $3.34 \times {10^{ - 27}}kg$ હોય તો બંનેના સંયોજન નો વેગ કેટલો થાય?View Solution
- 5એક હવામાં જતાં પદાર્થનો વેગ $(20 \hat{\mathrm{i}}+25 \hat{\mathrm{j}}-12 \hat{\mathrm{k}})$ છે તે અચાનક બે ભાગમાં વિભાજિત થાય છે જેમના દળનો ગુણોતર $1: 5$ છે.નાનો પદાર્થ $(100 \hat{\mathrm{i}}+35 \hat{\mathrm{j}} +8 \hat{\mathrm{k}})$ ના વેગથી ગતિ કરતો હોય તો મોટા પદાર્થનો વેગ કેટલો હશે?View Solution
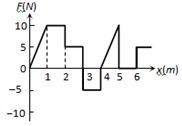
- 6બળ $F$ અને અંતર $ x$ વચ્ચેનો સંબંધ આકૃતિમાં દર્શાવ્યા પ્રમાણે છે તો પદાર્થ દ્વારા $x = 1 m$ થી $x = 5 m$ સ્થાંનાતર થવા માટે કરવું પડતું કાર્ય =….$J$View Solution
- 7$2 kg$ નો ટુકડો સમક્ષિતિજ તળિયે $4 m/s$ ની ઝડપે સરકે છે તે અસંકુચિત સ્પ્રિંગ સાથે અથડાય છે. તેનું ગતિક ઘર્ષણબળ $15 N$ અને સ્પ્રિંગ અચળાંક $10, 000 N/m $ છે. તો સ્પ્રિંગ કેટલા......$cm$ સંકોચન પામશે ?View Solution
- 8સ્થિર રહેલ $5 \;\mathrm{m}$ દળનો પદાર્થ ત્રણ ટુકડામાં વિભાજિત થાય છે. બે $m$ દળના પદાર્થ એકબીજાને લંબ રીતે $v$ વેગથી ગતિ કરે છે. તો આ પ્રક્રિયા દરમિયાન કેટલી ઉર્જા ($J$ માં) મુક્ત થઈ હશે?View Solution
- 9$2\,kg$ દળવાળો ગોળીયો પદાર્થ સ્થિર સ્થિતિમાંથી શરૂ કરી $5$ મી સેકન્ડના અંતે $10000\,J$ ગતિઉર્જા પ્રાપ્ત કરે છે. પદાર્થ પર લાગતું બળ $.............N$ છે.View Solution
- 10એક બોલ $ 'h'$ ઉંચાઈ પરથી મુક્ત રીતે પતન કરે છે. આ બોલ સતત પટકાઈને પાછો ફરે છે. પાછો ફરતો બોલ અટક્યા પહેલાં તેણે કેટલું અંતર કાપ્યું હશે?View Solution
