વધુ માત્રામાં $r$ ત્રિજ્યા ધરાવતા ટીપાં ભેગા થઈને એક મોટું $R$ ત્રિજ્યાનું ટીપું બનાવે છે.એંજીનિયર એવું મશીન બનાવે છે કે જેથી આ પ્રક્રિયા દરમિયાન મુક્ત થતી ઉષ્મા ટીપાની ગતિઉર્જામાં રૂપાંતર પામે.તો ટીપાનો વેગ કેટલો હશે? ($T=$ પૃષ્ઠતાણ , $\rho =$ ઘનતા)
AIEEE 2012,JEE MAIN 2014, Diffcult
b
When small droplets coelesce to form a bigger drop, energy released in this process is given by,
When small droplets coelesce to form a bigger drop, energy released in this process is given by,
\(4\pi {R^3}T\left[ {\frac{1}{r} - \frac{1}{R}} \right]\)
Where, \(R= radius\,of\,big\,drop\)
\(r=radius\,of\,small\,drop\)
\(T=surface\,tension\)
According to question
\(\frac{1}{2}m{v^2} = 4\pi {R^3}T\left[ {\frac{1}{r} - \frac{1}{R}} \right]\)
\( \Rightarrow \frac{1}{2}\left[ {\frac{4}{3}\pi {R^3}\rho } \right]{v^2} = 4\pi {R^3}T\left[ {\frac{1}{r} - \frac{1}{R}} \right]\)
\( \Rightarrow {V^2} = \frac{{6T}}{\rho }\left[ {\frac{1}{r} - \frac{1}{R}} \right] \Rightarrow V = {\left[ {\frac{{6T}}{\rho }\left( {\frac{1}{r} - \frac{1}{R}} \right)} \right]^{\frac{1}{2}}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionગુરુત્વમુકત અવકાશમાં પાણીમાં કેશનળી ડુબાડતાં પાણી ...
- 2$1\,mm$ ત્રિજયા અને $70 \times {10^{ - 3}}\,N/m$ પૃષ્ઠતાણ ધરાવતા ટીપાંના અંદરના અને બહારના દબાણનો તફાવત ....... $N/{m^{ - 2}}$ થાય.View Solution
- 3$0.28 \,mm$ આંતરિક વ્યાસ ધરાવતી એક કાચની કશનળીને પાણી ભરેલા પાત્રમાં શિરોલંબ રીતે મૂકેલી છે તો કેશનળીમાં પાણી પર કેટલું દબાણ લગાડવું જોઇએ કે જેથી કેશનળીમાંની પાણીની સપાટી પાત્રમાંના પાણીની સપાટી જેટલી થાય? (પાણીનું પૃષ્ઠતાણ $=0.07 \,N / m$ અને વાતાવરણ દબાણ $\left.=10^5 \,N / m ^2\right)$.View Solution
- 4View Solutionમશીન દ્વારા પરપોટા બનાવવામાં આવે છે. મશીન પરપોટાની ત્રિજયા સમયના સપ્રમાણમાં વધારતું હોય,તો પરપોટાનું અંદરનું દબાણ વિરુધ્ધ સમયનો આલેખ કેવો થાય?
- 5$8000$ નાના ટીપાંમાંથી મોટું ટીપું બને છે,અંતિમ પૃષ્ઠઊર્જા અને શરૂઆતની કુલ પૃષ્ઠઊર્જાનો ગુણોત્તર કેટલો થાય?View Solution
- 6$0.04 \mathrm{~cm}$ ઉંચાઈ ધરાવતો એક પ્રવાહી સ્તંભ કોઈ ચોક્કસ ત્રિજ્યા ધરાવતા સાબુના પરપોટાંનાં વધારાના દબાણને સંતુલીત કરે છે. જો પ્રવાહીની ધનતા $8 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$ અને સાબુના દ્રાવણ માટ પૃષ્ઠતાણ $0.28 \mathrm{Nm}^{-1}$ હોય તો સાબુના પરપોટાનો વ્યાસ. . . . . . . $\mathrm{cm}$.View Solution
(જો $\mathrm{g}=10 \mathrm{~ms}^{-2}$ હોય).
- 7View Solutionકેશનળીમાં પ્રવાહીની મેનિકસ બર્હિગોળ હોય,ત્યારે સંપર્કકોણ કેટલો હોય?
- 8View Solutionમશીન દ્વારા પરપોટા બનાવવામાં આવે છે. મશીન પરપોટાની ત્રિજયા સમયના સપ્રમાણમાં વધારતું હોય,તો પરપોટાનું અંદરનું દબાણ વિરુધ્ધ સમયનો આલેખ કેવો થાય?
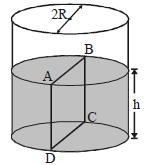
- 9$R$ ત્રિજ્યાના બીકરમાં $h$ ઊંચાઈ સુધી પાણી ભરવામાં આવે છે.પાણી ની ઘનતા $\rho$,પૃષ્ઠતાણ $T$ અને વાતાવરણનું દબાણ $P_0$ છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે એક આડછેદ $ABCD$ લો.આ આડછેદના એક બાજુના પાણી દ્વારા બીજી બાજુના પાણી પર કેટલા મૂલ્યનું બળ લાગે?View Solution
- 10$r$ ત્રિજયાવાળા એકસરખા અમુક ટીપાં ભેગા થઇ $R$ ત્રિજયા અને $V$ કદનું એક મોટું ટીંપું રચે છે. જો પ્રવાહીનું પૃષ્ઠતાણ $T$ હોય, તો .............View Solution
