વિધાન $A$ : જો $A, B, C, D$ એ અર્ધ વર્તુળ કેન્દ્ર $O$ પર ચાર બિંદુઓ એવા છે કે જેથી $|\overrightarrow{{AB}}|=|\overrightarrow{{BC}}|=|\overrightarrow{{CD}}|$ હોય, તો $\overrightarrow{{AB}}+\overrightarrow{{AC}}+\overrightarrow{{AD}}=4 \overrightarrow{{AO}}+\overrightarrow{{OB}}+\overrightarrow{{OC}}$
કારણ $R$ : સદીશ સરવાળાનો બહુકોણનો નિયમ $\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{A D}=2 \overrightarrow{A O}$ આપે છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પો પૈકી સૌથી વધારે યોગ્ય જવાબ પસંદ કરો.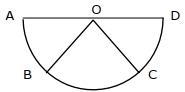 
JEE MAIN 2021, Diffcult
Download our app for free and get started
c
\(|\overrightarrow{A B}|=|\overrightarrow{B C}|=|\overrightarrow{C D}|\)
\(|\overrightarrow{A B}|=|\overrightarrow{B C}|=|\overrightarrow{C D}|\)
Here, \(O\) is the centre of semi- circle
\(\therefore|\overrightarrow{O A}|=|\overrightarrow{O B}|=|\overrightarrow{O C}|=|\overrightarrow{O D}|\)
Using vector law of addition, we can write,
\(\overrightarrow{ AB }=\overrightarrow{ AO }+\overrightarrow{ OB }\)
\(\overrightarrow{ AC }=\overrightarrow{ AO }+\overrightarrow{ OC }\)
\(\overrightarrow{ AD }=\overrightarrow{ AO }+\overrightarrow{ OD }=2 \overrightarrow{ AO }\)
After adding all, we get,
\(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D}=4 \overrightarrow{A O}+\overrightarrow{O B}+\overrightarrow{O C}\)
Reason \(R\) is the direct result of Polygon law of vector addition
Therefore, Polygon law is applicable in both but the equation given in the reason is not useful in explaining the assertion.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સદિશ $\vec{A}$ ઉત્તર દિશા તરફ છે અને સદિશ $\vec{B}$ ઊધર્વદિશા તરફ નિર્દેશિત છે . તો $\vec{A} \times \vec{B}$ કઈ દિશા તરફ નિર્દેશિત છે ?View Solution
- 2View Solutionનીચેનામાંથી કઈ અદીશ રાશિ છે?
- 3બે સદિશો $\vec{A}$ અને $\vec{B}$ નો પરિણામી સદિશ $\vec{A}$ ને લંબ અને તનું મૂલ્ય $\vec{B}$ ના કરતાં અડધુ છે. $\vec{A}$ અન $\vec{B}$ વચ્ચેનો કોણ ............. હશે.View Solution
- 4$\left| {{{\vec A}_1}} \right| = 3,\,\left| {\vec A_2} \right| = 5$, અને $\left| {{{\vec A}_1} + {{\vec A}_2}} \right| = 5$ આપેલ છે. $\left( {2{{\vec A}_1} + 3{{\vec A}_2}} \right)\cdot \left( {3{{\vec A}_1} - 2{{\vec A}_2}} \right)$ નું મૂલ્ય કેટલું થાય?View Solution
- 5સમાંતર બાજુ ચતુષ્કોણ કે જેના વિકર્ણો ${3\hat i}\,\, + \,\,\hat j\,\, - \,\,2\hat k$ અને $\hat i\,\, - \,\,3\hat j\,\, + \;\,4\hat k$ છે. તો તેનું ક્ષેત્રફળ શોધો.View Solution
- 6View Solutionઅલગ અલગ સમતલના કેટલા સદિશોનો સરવાળો કરતાં પરિણામી શૂન્ય મળે ?
- 7$\vec A\, = \,(\hat i\, + \,\hat j)$ અને $\vec B\, = \,(2\hat i\, - \,\hat j)$ આપેલ છે. સમતલ સદિશ $\vec C$ નું મૂલ્ય શેના વડે આપવામાં આવે, કે જેથી $\vec A\cdot \vec C\, = \,\vec B\cdot \vec C\, = \vec A\cdot \vec B$ થાય?View Solution
- 8જો $\overrightarrow{ P } \times \overrightarrow{ Q }=\overrightarrow{ Q } \times \overrightarrow{ P }$ હોય તો $\overrightarrow{ P }$ અને $\overrightarrow{ Q }$ વચ્ચેનો કોણ $\theta\left(0^{\circ} < \theta < 360^{\circ}\right)$ છે. જ્યાં $\theta$ નું મૂલ્ય ....... ડિગ્રી હશે.View Solution
- 9ક્યાં સદિશને પરિણામી સદિશ $\mathop P\limits^ \to \,\, = \,\,2\hat i\,\, + \;\,7\hat j\,\, - \,\,10\hat k\,\,$ અને $\,\,\mathop Q\limits^ \to \,\, = \,\,\hat i\,\, + \;\,2\hat j\,\, + \;\,3\hat k$ માં ઉમેરવામાં આવે તો તે $X$- અક્ષની દિશામાં એકમ સદિશ આપે.View Solution
- 10જો $ |\vec A \times \vec B| = \sqrt 3 \vec A.\vec B $ હોય, તો $ |\vec A + \vec B| $ નું મૂલ્ય શું થાય?View Solution