કારણ : બે સમાન જાડાઈ ધરાવતી ધાતુની પ્લેટની સમતુલ્ય ઉષ્માવાહકતા $\frac{1}{K} = \frac{1}{{{K_1}}} + \frac{1}{{{K_2}}}$ સૂત્ર મુજબ અપાય છે.
For equivalent thermal coductivity, the relation is
\(\frac{1}{{{K_R}}} = \frac{1}{{{K_1}}} + \frac{1}{{{K_2}}};If\,{K_1} = {K_2} = k\)
\(\frac{1}{{{k_R}}} = \frac{1}{K} + \frac{1}{K} = \frac{2}{K} \Rightarrow {K_R} = \frac{K}{2}\)
Which is less than \(K\).
\(If\,{K_1} > {K_2}\,suppose\,{K_1} = {K_2} + x\)
\(\frac{1}{K} = \frac{1}{{{K_1}}} + \frac{1}{{{K_2}}} = \frac{{{K_2} + {K_1}}}{{{K_1}{K_2}}}\)
\( \Rightarrow \frac{1}{K} = \frac{{{K_2} + {K_2} + x}}{{\left( {{K_2} + x} \right){K_2}}} \Rightarrow K = \frac{{K_2^2 + {K_2}x}}{{2{K_2} + x}}\)
\(Now,\,{K_2} - K = {K_2} - \frac{{K_2^2 + {K_2}x}}{{2{K_2} + x}}\)
\( = \frac{{2K_2^2 + {K_2}x - K_2^2 - {K_2}x}}{{\left( {2{K_2} + x} \right)}}\)
\( = \frac{{K_2^2}}{{2{K_2} + x}} = positive\)
\(So.{K_2} > K,so\,the\,value\,of\,K\,is\,smaller\,than\,\)
\({K_2}\,and\,{K_1}.\)
Download our appand get started for free
Similar Questions
- 1$227°C$ તાપમાને કાળો પદાર્થ $20\,\, cal\, m^{-2} \,s^{-1}$ ના દરથી ઉષ્મા વિકિરીત કરે છે જ્યારે તેનું તાપમાન $727°C$ કરવામાં આવે ...... $cal \,\, m^{-2}\, s^{-1}$ ત્યારે ઉષ્મા વિકીરીત કરશે$?$View Solution
- 2સમાન જાડાઇ ધરાવતા બે બ્લોકની ઉષ્મા વાહકતાનો ગુણોત્તર $1:4$ છે. બંને બ્લોક સંપર્કમાં રાખવામાં આવે છે. પ્રથમ બ્લોકના મુકત છેડાનું તાપમાન $ 0^o C $ અને બીજા બ્લોકના મુકત છેડાનું તાપમાન $ {100^o}C $ છે. તો સંપર્ક સપાટીનું તાપમાન....... $^oC$View Solution
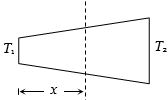
- 3View Solutionઅનિયમિત આડછેદ ધરાવતા વાહકમાંથી ઉષ્મા પસાર થાય છે.તો ઉષ્મા પ્રવાહ વિરુધ્ધ અંતરનો આલેખ.
- 4View Solutionસંપૂર્ણ કાળો પદાર્થ ........ છે.
- 5જો $\lambda_{ m }$ એ $T\;K$ તાપમાને રહેલા કાળા પદાર્થમાંથી મહત્તમ ઉત્સર્જાતા વિકિરણની તરંગલંબાઈ દર્શાવે, તો .......View Solution
- 6જો સૂર્યનું તાપમાન કદાચ $T$ થી વધીને $2\,T$ થાય અને તેની ત્રિજયા $R$ થી વધીને $2\,R$ થાય,તો પૃથ્વી દ્વારા મેળવાતી ઊર્જા પહેલા કરતાં કેટલા ગણી થાય?View Solution
- 7વર્તૂળાકાર હીટરથી અંતરે કાળું ધાતુનું વરખ રાખેલું છે. વરખ દ્વારા શોષાતો પાવર $P$ છે. જો હીટરનું તાપમાન અને અંતર બમણું કરવામાં આવે ત્યારે વરખ દ્વારા શોષાતો પાવર ..... $P$ થશે.View Solution
- 8View Solutionજ્યારે આપણે એરકન્ડીશન વાળા ઓરડામાં દાખલ થઈએ ત્યારે ઠંડક અનુભવીએ છીએ. આ .....વડે સમજાવી શકાય છે.
- 9ગરમ પાણીનું તાપમાન $ {61^o}C $ થી $ {59^o}C $ થતા $4$ minutes લાગે છે,તો પદાર્થનું તાપમાન $ {51^0}C $ થી $ {49^0}C $ થતાં લાગતો સમય ....... $\min$ શોધો.વાતાવરણનું તાપમાન $ {30.0^o}C $ છે.View Solution
- 10ઉષ્મીય રીતે અલગ કરેલા એક સળિયાનાં બંને છેડાનાં તાપમાનો અનુક્રમે $T _{1}$ અને $T _{2}$ છે. સળિયો $l_{1}$ અને $l_{2}$ એમ બે વિભાગોના જોડાણથી બનેલો છે. બંને દ્રવ્યોની ઉષ્માવાહકતા $k _{1}$ અને $k _{2}$ છે. તો બે ભાગોની જોડતી સપાટીએ તાપમાન કેટલું થાય?View Solution

