વિદ્યુતક્ષેત્ર શોધવા ગાઉસનો નિયમ $|\overrightarrow{\mathrm{E}}|=\frac{q_{\mathrm{enc}}}{\varepsilon_{0}|\mathrm{A}|}$ વાપરવામાં આવે છે.જ્યાં $\varepsilon_{0}$ શૂન્યાવકાશની પરમિટિવિટી, $A$ ગાઉસીયન સપાટીનું ક્ષેત્રફળ અને $q_{enc}$ એ ગાઉસીયન સપાટીની અંદર રહેલ વિજભાર છે.ઉપરનું સૂત્ર ક્યારે વાપરવામાં આવે છે?
JEE MAIN 2020, Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉગમ બિંદુથી $x-$ અક્ષ પર ત્રણ વિદ્યુતભારો $+Q, q$ અને $+Q $ અનુક્રમે $0,\frac d2$ અને $d$ આગળ મુકેલ છે. જો $x=0$ આગળ મુકેલ $+Q$ દ્વારા અનુભવાતું કુલ બળ શૂન્ય હોય તો $q$ નું મૂલ્ય કેટલું હશે.View Solution
- 2દરેક $m$ જેટલું દળ અને $q$ જેટલો વિદ્યુતભાર ધરાવતા બે એકસમાન ટેનિસ બોલને $l$ લંબાઈની દોરી વડે જડિત બિંદુથી લટકવવામાં આવેલ છે. જ્યારે શિરોલંબ સાથે દરેક દોરી નાનો કોણ $\theta$ રચતી હોય તો ત્યારે સંતુલન સ્થિતિમાં અંતર .......... હશે?View Solution
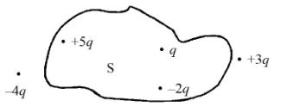
- 3પાંચ વિદ્યુતભારો $+q,+5 q,-2 q,+3 q$ અને $-4 q$ ને આક્રૂત્તિમાં દર્શાવ્યા અનુસાર ગોઠવવામાં આવ્યા છે.View Solution
સપાટી $s$ માંથી પસાર થતું આ વિદ્યુતભારોની ગોઠવણીને કારણે સંકળાયેલ ફ્લક્સ...........છે.
- 4$\rho (r)\,\, = \,\,{\rho _0}\left( {\frac{5}{4}\, - \,\,\frac{r}{R}} \right)$ એ વિદ્યુતભારની ઘનતા સાથે બદલાતું ગોળીય સંમિત વિદ્યુતભારનું વિતરણ આપે છે. જે $r = R$, અને $\rho (r)\,\, = \,\,0$ માટે $r > R$ જ્યાં $r$ એ ઉગમબિંદુથી અંતર છે. ઉગમબિંદુથી $r$ અંતરે $(r < R)$ વિદ્યુતક્ષેત્ર ....... દ્વારા આપવામાં આવે છે.View Solution
- 5શાંત વાતાવરણમાં વિદ્યુતક્ષેત્ર તીવ્રતા $100 \,V / m$ છે, તો પૃથ્વીની સપાટી પર કુલ વિદ્યુતભાર .............. $C$ છે (પૃથ્વીની ત્રીજ્યા $6400 \,km$ છે.)View Solution
- 6View Solutionપોલરાઈઝેશનની તીવ્રતાનું પારિમાણિક સૂત્ર કયું છે?
- 7$2 \,m$ અંતરે રહેલા બે સમાન વિદ્યુતભાર $q$ ધરાવતા બે સ્થિર કણની વચ્ચે એક $1 \,{mg}$ દળ અને $q$ વિદ્યુતભાર ધરાવતો કણ પડેલો છે. જો મુક્ત વિદ્યુતભારને તેના સમતોલન સ્થાનેથી $x\;(x\, < 1\, {m})$ જેટલું થોડુક સ્થાનાંતર કરવવામાં આવે, તો કણ સરળ આવર્ત ગતિ કરે છે. જો ${q}^{2}=10\, {C}^{2}$ હોય તો આ દોલનોની કોણીય આવૃતિ $....\,\times 10^{8}\, {rad} / {s}$ થાય.View Solution
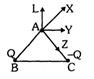
- 8આપેલ આકૃતિ માટે $A$ બિંદુ આગળ વિદ્યુતક્ષેત્રની દિશા ......... હશે.View Solution
- 9$Z$ પરમાણું ક્રમાંક ધરાવતા પરમાણુને $R$ ત્રીજ્યાના ગોળાની અંદર એકસમાન વિતરીત ઋણ વિદ્યુતભારના વિતરણ વડે ઘેરાયેલો અને કેન્દ્ર પાસે ઘન વિદ્યુતભાર ધરાવે છે તેમ ધ્યાનમાં લો. પરમાણુની અંદર કેન્દ્રથી $r$ અંતરે આવેલા બિંદુુએ વિદ્યુતક્ષેત્ર કેટલું છે?View Solution
- 10$a$ બાજુવાળા ચોરસના શિરોબિંદુ પર સમાન વિદ્યુતભાર $q$ મૂકવામાં આવે છે.તો એક વિદ્યુતભાર પર કેટલું બળ લાગે?View Solution