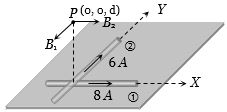
$X$ અક્ષ અને $Y$ - અક્ષ પર મૂકેલા બે અનંત લંબાઇના તારમાંથી $8A$ અને $6A$ પ્રવાહ પસાર થાય છે,તો $ P\,(0,\,0,\,d)\,m $ બિંદુ પર ચુંબકીયક્ષેત્ર કેટલું થાય?
Diffcult
d
(d) Magnetic field at \(P\) due to wire \(1\), \({B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\,(8)}}{d}\)
and due to wire \(2\), \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\,(6)}}{d}\)
\(==>\) \({B_{net}} = \sqrt {B_1^2 + B_2^2} = \sqrt {{{\left( {\frac{{{\mu _0}}}{{4\pi }}.\frac{{16}}{d}} \right)}^2} + {{\left( {\frac{{{\mu _0}}}{{4\pi }}.\frac{{12}}{d}} \right)}^2}} \)
\( = \frac{{{\mu _0}}}{{4\pi }} \times \frac{2}{d} \times 10 = \frac{{5{\mu _0}}}{{\pi d}}\)
(d) Magnetic field at \(P\) due to wire \(1\), \({B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\,(8)}}{d}\)
and due to wire \(2\), \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\,(6)}}{d}\)
\(==>\) \({B_{net}} = \sqrt {B_1^2 + B_2^2} = \sqrt {{{\left( {\frac{{{\mu _0}}}{{4\pi }}.\frac{{16}}{d}} \right)}^2} + {{\left( {\frac{{{\mu _0}}}{{4\pi }}.\frac{{12}}{d}} \right)}^2}} \)
\( = \frac{{{\mu _0}}}{{4\pi }} \times \frac{2}{d} \times 10 = \frac{{5{\mu _0}}}{{\pi d}}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઓહમના નિયમમાં એમિટર અને વૉલ્ટમીટર ને અવરોધ શ્રેણી અથવા સમાંતરમાં જોડવામાં આવે છે.
- 2View Solutionનીચેના પૈકી કયું વિધાન ખોટું છે?
- 3એક ગેલ્વેનોમીટર પૂર્ણ આવર્તન માટે $10^{-4}\, A$ જેટલો પ્રવાહ માપી શકે છે. તેને $0 -5\, V$ માપી શકે તેવા વોલ્ટમીટરમાં ફેરવવા માટે શ્રેણીમાં $2\, M\,\Omega $ જેટલો અવરોધ જોડાવો પડે છે.તો આ ગેલ્વેનોમીટરને $0-10\, mA$ પ્રવાહ માપી શકે તેવા એમીટરમાં ફેરવવા માટે કેટલા ......$\Omega $ શંટ અવરોધ જોડવો પડે?View Solution
- 4એકી-આયનીકૃત મેગ્નેશીયમ પરમાણુ $( A=24)$ ને $5 \,keV$ ની ગતિઊર્જ જેટલો પ્રવેગિત કરવામાં આવે છે, અને $0.5 \,T$ મૂલ્ય ધરાવતા યુંબકીકીય ક્ષેત્ર $B$ માં લંબરૂપે પ્રક્ષિપ્ત (ફેંકવામા) આવે છે. ગતિપથની ત્રિજ્યા .............. $cm$ થશે.View Solution
- 5$Z$ અક્ષ પર મૂકેલા તારમાંથી ૠણ $Z$ - દિશામાં $I$ પ્રવાહ પસાર થાય છે.તો બિંદુ $(x, y)$ આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 6$R$ જેટલી બહારની ત્રિજ્યા ધરાવતા એક અત્યંત લાંબા (અનંત) પોલા વાહક નળાકાર તેની લંબાઈની દિશામાં નિયમિત પ્રવાહ ધનતા ધરાવે છે. નળાકારની અક્ષથી ત્રિજ્યાવર્તી અંતર $(r)$ ના વિધેય તરીકે ચુંબકીય ક્ષેત્ર $(B)$ ને ............ સાચી રીતે દશાવે છે.View Solution
- 7બે તાર $AOB$ અને $COD$ ને લંબ રાખીને તેમાંથી $ {i_1} $ અને $ {i_2} $ પ્રવાહ પસાર કરવામાં આવે છે.તો બિંદુ $O$ થી $ABCD$ સમતલને લંબ $a$ અંતરે બિંદુ $P$ આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
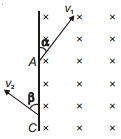
- 8$m$ દળનો અને $-q$ વિદ્યુતભાર ધરાવતો એક કણ એકરૂપ ચુંબકીય ક્ષેત્રમાં $A$ પાસે $v_1$ ઝડપથી $\alpha$ ખૂણે દાખલ થાય છે અને $C$ પાસે $v_2$ ઝડપથી આકૃતિમાં દર્શાવ્યા પ્રમાણે $\beta$ ખૂણે બહાર આવે તોView Solution
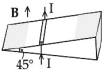
- 9આકૃત્તિમાં દર્શાવ્યા અનુસાર, $0.45 \,kg m ^{-1}$ જેટલી રેખીય ઘનતા ઘરાવતો એક ધાતુનો સઇિયો એક લીસા ઢોળાવ (ઢળતા સમતલ), કે જે સમક્ષિતિજ સાથે $45^{\circ}$ નો કોણ બનાવે છે, ની ઉપર સમક્ષિતિન રાખવામાં આવે છે. સળિયા પર જ્યારે ઉધ્વ્ દિશામાં શિરેલંબ $0.15 \,T$ જેટલું ચુંબકીય ક્ષેત્ર પ્રવર્તતું હોય, ત્યારે સળિયાને સ્થિર રાખવા માટે જરૂરી લઘુત્તમ પ્રવાહ ......... હશે. { $g =10 \,m / s ^{2}$ નો ઉપયોગ કરે.}View Solution
- 10View Solutionનીચેના પૈકી કયું વિધાન ખોટું છે?
