$x$ અક્ષની દિશામાં મુક્ત રીતે ગતિ કરતા $1 kg $ દળના કણની સ્થિતિ ઊર્જા $V(x)\,\, = \,\,\left( {\frac{{{x^4}}}{4}\, - \,\,\frac{{{x^2}}}{2}} \right)\,J$સૂત્રથી આપી શકાય કણની કુલ યાંત્રિક ઊર્જા $2 J $ છે. તો કણની મહત્તમ ઝડપથી $ (m/s)$ માં કેટલી હશે ?
Diffcult
a
\({\text{V}}\,\, = \,\,\frac{{{{\text{x}}^{\text{4}}}}}{4}\,\, - \,\frac{{{x^2}}}{2}\,\, \Rightarrow \,\,\frac{{dV}}{{dx}}\,\, = \,\,{x^3}\,\, - \,\,x\,\, = \,\,0\,\, \Rightarrow \,\,x\,\, = \,\,0,\,1,\,\, - \,1\)
\({\text{V}}\,\, = \,\,\frac{{{{\text{x}}^{\text{4}}}}}{4}\,\, - \,\frac{{{x^2}}}{2}\,\, \Rightarrow \,\,\frac{{dV}}{{dx}}\,\, = \,\,{x^3}\,\, - \,\,x\,\, = \,\,0\,\, \Rightarrow \,\,x\,\, = \,\,0,\,1,\,\, - \,1\)
\(x\,\, = \,\, \pm 1\,\,\) પાસે \(v \) ન્યૂનતમ છે .
\({V_{\min }}\, = \,\,{V_{x\,\, = \,\, \pm \,1}}\,\, = \,\,\frac{{{{\left( { \pm \,1} \right)}^4}}}{4}\,\, - \,\,\frac{{{{\left( { \pm \,\,1} \right)}^2}}}{2}\,\, = \,\, - \frac{1}{4}\,\,J\)
આ બિંદુઓ પર ગતિઉર્જા મહતમ છે .
\(K{E_{\max }}\,\, + \,\,{V_{\min }}\) કુલ યંત્રિકઉર્જા
\(K{E_{\max }}\,\, - \,\,\frac{1}{4}\, = \,\,2\,\, \Rightarrow \,\,\frac{1}{2}\,\,m{v^2}_{\max }\,\, = \,\,2\,\, + \;\,\frac{1}{4}\,\, = \,\,\frac{9}{4}\)
\( \Rightarrow \,\,\frac{1}{2}\,\, \times \,\,1\,\, \times \,\,{v^2}_{\max }\,\, = \,\,\frac{9}{4}\,\, \Rightarrow \,\,{v_{\max }}\,\, = \,\frac{3}{{\sqrt 2 }}\,\,m/s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$1\,m$ લંબાઇ ધરાવતી દોરી પર $2\,kg$ નો પદાર્થ બાંધીને શિરોલંબ વર્તુળમાં $4\,m/sec$ ની અચળ ઝડપથી ફેરવવામાં આવે છે.તો દોરીમાં તણાવ $52\, N$ કયાં સ્થાને થાય?View Solution
- 2પદાર્થ પર $4\hat i + \hat j + 3\hat k\,N$ બળ લાગતાં તેનું સ્થાનાંતર $3\hat i + 2\hat j - 6\hat k$ થી $14\hat i + 13\hat j + 9\hat k$ થાય છે.તો કાર્ય .......... $J$ મેળવે.View Solution
- 3એક $m$ દળનો દડો $v$ વેગ સાથે, એક દિવાલથી $60^{\circ}$ ના ખૂણા પર સ્થિતિસ્થાપક રીતે અથડાય છે તો દિવાલની સાપેક્ષે દડાનાં વેગમાનમાં થતાં ફેરફરનું મૂલ્ય શું છે?View Solution
- 4$3 kg$ દળ ધરાવતા અને $2 Ns$ જેટલુ વેગમાન ધરાવતા પદાર્થની ગતિઊર્જા કેટલી હશે?View Solution
- 5View Solutionવિધાન: ઘર્ષણબળો એ સંરક્ષિ બળો છે.
કારણ: સ્થિતિઉર્જા ને ઘર્ષણબળો સાથે જોડી શકાય.
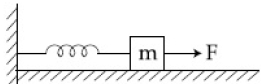
- 6$m$ દળ ધરાવતા એક ચોસલાને $k$ સ્પ્રિંગ અચળાંક ધરાવતી એક દળરહિત સ્પ્રિંગ વડે જોડવામાં આવેલ છે. આ ચોસલાને લીસી સમક્ષિતિજ સપાટી પર મુકવામાં આવે છે અને સ્પ્રિંગના બીજા છેડાને આકૃતિમાં બતાવ્યા પ્રમાણે જડવામાં આવેલ છે. જો અચળ બળથી ચોસલાને ખેંચવામાં આવે તો ચોસલા દ્વારા ધારણ કરવામાં આવતી મહત્તમ ઝડ૫ _______ થાય.View Solution
- 7કણ પર $F$ બળ લાગતાં તે બળની દિશામાં $v$ વેગથી ગતિ કરે છે. તો પાવર કેટલો થાય?View Solution
- 8એક માણસની ગતિઊર્જા તેનાથી અડઘું દળ ઘરાવતા છોકરાથી અડઘી છે.જો માણસની ઝડપમાં $ 1 m/s$ નો વઘારો કરવામાં આવે તો બંનેની ગતિઊર્જા સમાન થાય છે. માણસની મૂળ ઝડપView Solution
- 9એવું જોવા મળે છે,કે સ્થિર રહેલા ડયુટેરિયમ સાથે જયારે ન્યુટ્રોન સ્થિતિસ્થાપક એક રેખિક અથડામણ અનુભવે છે,ત્યારે તેની ઊર્જામાં થતો આંશિક વ્યય $P_d$ છે.પણ જયારે તે સરખી સ્થિતિમાં સ્થિર સ્થિતિમાં રહેલ કાર્બન ન્યુકિલયસ જોડે અથડામણ અનુભવે છે,ત્યારે ઊર્જામાં થતો આંશિક વ્યય $P_c $ છે.$P_d$ અને $P_c$ ની અનુક્રમે કિંમત _______.View Solution
- 10એક પાણીનો પંપ પેટ્રોલથી ચાલે છે જે $30 m.$ ઉંડાઈએથી $0.5 m^3/min$ ના દરે પાણી બહાર ખેંચે છે. જો પંપની કાર્યક્ષમતા $70\%$ હોય તો એન્જિન વડે ઉત્પન્ન થતો પાવર ......... $W$ હશે .View Solution
