$(x - y)$ સમતલમાં એક લંબચોરસ, એક ચોરસ, એક વર્તુળાકાર અને લંબગોળાકાર લૂપ $\overrightarrow{V}=v \hat{i}$ ના અચળ વેગથી નિયમિત ચુંબકીય ક્ષેત્રની બહાર જઈ રહ્યા છે. ચુંબકીય ક્ષેત્રની દિશા ઋણ $z$ અક્ષ ની દિશામાં છે. ક્ષેત્રમાંથી બહાર આવવાની પ્રક્રિયામાં, આ લૂપમાં પ્રેરિત $e.m.f.$ અચળ રહેશે નહીં
AIPMT 2009, Easy
a
Once a rectangular loop or a square loop is being drawn out of the field, the rate of cutting the lines of field will be a constant for a square and rectangle, but not for circular or elliptical areas.
Once a rectangular loop or a square loop is being drawn out of the field, the rate of cutting the lines of field will be a constant for a square and rectangle, but not for circular or elliptical areas.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
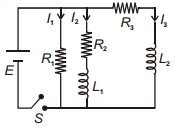
- 1આકૃતિ $L-R$ સર્કીટ દર્શાવે છે. જ્યારે સ્વીય $S$ બંધ હોય ત્યારે અવરોધ $R_1, R_2$ અને $R_3$ માં વિદ્યુત પ્રવાહ પસાર થાય છે. તથા તે $I_1, I_2$ અને $I_3$ અનુક્રમે છે.તો $t =0\; s \;\;I_1, I_2$ અને $I_3$ નાં મૂલ્યોView Solution
- 2View Solutionજ્યારે બે ગુચળાને એકબીજાની નજીક રાખવામા આવે ત્યારે તેમની જોડનું અન્યોન્ય પ્રેરકત્વ કોના પર આધાર રાખે?
- 3સ્ટેપ ડાઉન ટ્રાન્સફોર્મર $1000\,V$ પર લગાવતાં $120\,V$ પર $20\,A$ પ્રવાહ સપ્લાય કરે છે,જો ટ્રાન્સફોર્મરની કાર્યક્ષમતા $80\%$ હોય,તો પ્રાથમિક ગૂંચળામાં પ્રવાહ કેટલા .......$A$ હશે?View Solution
- 4એક $ac$ જનરેટરમાં $14 \times 10^{-2}$ ક્ષેત્રફળ વાયુ અને $100$ આંટા ધરાવતું લંબચોરસ ગૂંચળું $3.0\,T$ મૂલ્યના સમાન ચુંબકીય ક્ષેત્રમાં અક્ષને લંબ દિશામાં $360$ પરિભ્રમણ મિનિટથી ભ્રમણ કરે છે. તો ઉત્પન્ન થયેલ મહત્તમ $emf$ નું મૂલ્ય $............V$ થશે. ($\left.\pi=\frac{22}{7}\right.$ લો.)View Solution
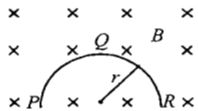
- 5$r$ ત્રિજ્યાની પાતળી અર્ધવર્તુળાકાર વાહક રિંગ $(PQR)$ સમક્ષિતિજ ચુંબકીય ક્ષેત્ર $B$ માં પડી રહી છે. તેનું સમતલ આકૃતિમાં બતાવ્યા પ્રમાણે ઊભું રહે છે. જ્યારે રીંગની ઝડપ $v$ હોય, ત્યારે તેના બે છેડા વચ્ચે ઉદ્ભવતા સ્થિતિમાનનો તફાવત કેટલો હશે?View Solution
- 6જો $N$ કોઈલના આંટાની સંખ્યા હોય, તો તેનું આત્મપ્રેરકત્વ કઈ રીતે બદલાય?View Solution
- 7$60 \mathrm{~cm}$ લંબાઈનો એક સળિયો $20 \mathrm{rots}^{-1}$ ના નિયમિત કોણીય વેગથી તેના લંબ દ્રીભાજકને અનુલક્ષીને $0.5 T$ ના નિયમિત ચુંબકીય ક્ષેત્રમાં ભ્રમણ કરે છે. ચુંબકીય ક્ષેત્રની દિશા ભ્રમણ અક્ષને સમાંતર છે. સળિયાના બે છેડાઓ વચ્ચે સ્થિતમાનનો તફાવત . . . . . .$\mathrm{V} $છે.View Solution
- 8$5000$ આંટા અને $ 0.25\,{m^2} $ ક્ષેત્રફળ ધરાવતી કોઇલ જનરેટરમાં વાપરવામાં આવે છે,કોઇલ $0.2$ $ W/{m^2} $ ચુંબકીયક્ષેત્રમાં $100$ પરિભ્રમણ/sec ની કોણીય ઝડપથી ભ્રમણ કરતાં કેટલા ......$kV$ મહત્તમ $emf$ ઉત્પન્ન થાય?View Solution
- 9પ્રેરક (ઈન્ડક્ર) માં વહેતો પ્રવાહ $I=(3 t+8) A$ થી આપી શકાય છે, જ્યાં $t$ એ સકેન્ડમાં છે. ઈન્ડક્ટરમાં ઉત્પન પ્રેરિત emf નું મૂલ્ય $12 \mathrm{mV}$ છે. ઈન્ડફટર માટે આત્મ્પ્રેરક્ત્વ. . . . . . $\mathrm{mH}$ થશે.View Solution
- 10$R$ અવરોધવાળી કોઇલમાં $ \Delta t $ સમયમાં ફલક્સનો ફેરફાર $ \Delta \phi $ હોય, તો આ સમયમાં કોઇલના કોઈ બિંદુ પાસેથી કેટલો વિદ્યુતભાર $Q$ પસાર થાય?View Solution
