$Y$ યંગ મોડ્યુલસ ધરાવતા દ્રવ્યમાંથી એક ઘટતી ત્રિજ્યા ધરાવતો શંકુ આકારનો તાર બનાવવામાં આવે છે જેની મૂળભૂત લંબાઈ $L$ અને તારના ઉપરના અને નીચેના ભાગની ત્રિજ્યા અનુક્રમે $R$ અને $3R$ છે.તારણો ઉપરનો ભાગ દઢ આધાર સાથે અને નીચેના ભાગ સાથે $M$ દળ લટકાવેલ છે તો તારની નવી વિસ્તૃત લંબાઈ કેટલી થશે?
JEE MAIN 2016, Diffcult
c
Consider a small element \(dx\) of radius \(r\),
Consider a small element \(dx\) of radius \(r\),
\(r = \frac{{2R}}{L}x + R\)
At equilibrium change in length of the wire
\(\int\limits_0^l {dL = \int {\frac{{Mgdx}}{{\pi {{\left[ {\frac{{2R}}{L}x + R} \right]}^2}y}}} } \)
Taking limit from \(0\) to \(L\)
\(\Delta L = \frac{{Mg}}{{\pi y}} - \frac{1}{{\left[ {\frac{{2Rx}}{L} + R} \right]_0^L}} \times \frac{L}{{2R}} = \frac{{MgL}}{{3\pi {R^2}y}}\)
The equilibrium extended length of wire
\( = L + \Delta L\)
\( = L + \frac{{MgL}}{{3\pi {R^2}Y}} = L\left( {1 + \frac{1}{3}\frac{{Mg}}{{\pi Y{R^2}}}} \right)\)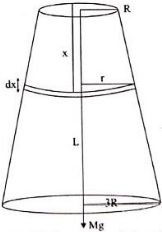
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1તાર પર બળ લગાવતા તેની લંબાઈમાં $1 mm$ નો વધારો થાય છે. બીજા સમાન દ્રવ્ય અને લંબાઈ ધરાવતો પરંતુ જેના આડછેદની ત્રિજ્યા અડધી છે તેના પર પહેલા કરતાં બમણું બળ લગાવવામાં આવે તો તારની લંબાઈમાં($mm$ માં) કેટલો વધારો થાય?View Solution
- 2દ્રવ્યનો પોઈસનનો ગુણોત્તર $0.5$ છે જો આ તારમાં બળ આપવામા આવે તો તેના આડછેદમાં $4 \%$ જેટલો ઘટાડો થાય. છે. તો તેના લંબાઈમાં થતો વધારો .............. $\%$View Solution
- 3View Solutionઘન પદાર્થમાં આંતરઆણ્વિય બળ ...
- 4વાયુની સમતાપી સ્થિતિસ્થાપકતા કોને બરાબર હોય $?$View Solution
- 5સમાન દ્રવ્યના બનેલા તાર $A$ અને $B$ પર સમાન બળ $2\,N$ લગાવીને તેમની લંબાઈ $2 \,mm$ અને $4\, mm$ વધારવામાં આવે છે.$B$ની ત્રિજ્યા $A$ કરતા ચાર ગણી છે,બંનેની લંબાઇનો ગુણોતર $a / b\,=\,1 / x$ હોય તો $x=\,.......$View Solution
- 6યંગ મોડયુલસ $Y,$ બલ્ક મોડયુલસ $K$ અને આકાર સ્થિતિસ્થાપકતા અંક $\eta $ વચ્ચેનો સંબંધ $?$View Solution
- 7View Solutionનીચેનામાથી કયો સંબંધ સાચો છે.
- 8$A$ અને $B$ તાર સમાન દ્રવ્યના બનેલા છે અને ત્રિજ્યાનો ગુણોત્તર $2: 1$ અને લંબાઈનો ગુણોત્તર $4: 1$ છે. તો બંને તારમાં લંબાઈમાં એકસમાન ફેરફાર કરવા માટે તેના જરૂરી બળનો ગુણોત્તર = ?View Solution
- 9એક ક્રેનમાં ભાર ઊંચકવા વપરાતા દોરડાના આડછેદનું ક્ષેત્ર $2.5 \times 10^{-4} m ^2$ છે. ટ્રેનની મહત્તમ ઊંચકવાની ક્ષમતા $10$ મેટ્રીક ટન છે. ક્રેનની મહત્તમ ઊંચકવાની ક્ષમતા $25$ મેટ્રીક ટન કરવી હોય તો દોરડાના આડછેદનું ક્ષેત્રફળ $\dots \times 10^{-4} \,m ^{2}$ જોઈશે. $(g=10 ms { }^{-2}$ લો)View Solution
- 10$2 \,m$ લંબાઈ ધરાવતા તારના એક છેડે $10 \,kg$ નો દળ લટકાવવામા આવે. છે ત્યારે તે $10 \,mm$ કેટલું ખેચાય છે.આ દરમિયાન સંગ્રહ પામતી સ્થિતિસ્થાપક સ્થિતિ ઉર્જા = .............. $J$ (take $g=10 \,m / s ^2$ લો)View Solution
