યંગના પ્રયોગમાં સફેદ પ્રકારનો ઉપયોગ કરવામાં આવે છે. બે સ્લિટ વચ્ચેનું અંતર $b$ છે.સ્લિટ અને પડદા વચ્ચે નું અંતર $d (d>> b)$ છે. સ્લિટની બરાબર સામે ગેરહાજર તરંગલંબાઈ
IIT 1984,AIIMS 1995, Diffcult
d
(d) Path difference between the rays reaching infront of slit \(S_1\) is.
(d) Path difference between the rays reaching infront of slit \(S_1\) is.
\({S_1}P - {S_2}P = {({b^2} + {d^2})^{1/2}} - d\)
For distructive interference at \(P\)
\({S_1}P - {S_2}P = \frac{{(2\,n - 1)\lambda }}{2}\)
i.e., \({({b^2} + {d^2})^{1/2}} - d = \frac{{(2n - 1)\lambda }}{2}\)
\( \Rightarrow d\,{\left( {1 + \frac{{{b^2}}}{{{d^2}}}} \right)^{1/2}} - d = \frac{{(2n - 1)\lambda }}{2}\)
\( \Rightarrow d\,\left( {1 + \frac{{{b^2}}}{{2{d^2}}} + ......} \right) - d = \frac{{(2n - 1)\lambda }}{2}\)
(Binomial Expansion)
\( \Rightarrow \frac{b}{{2d}} = \frac{{(2n - 1)\lambda }}{2} \Rightarrow \lambda = \frac{{{b^2}}}{{(2n - 1)d}}\)
For \(n = 1,\;2............,\;\lambda = \frac{{{b^2}}}{d},\;\frac{{{b^2}}}{{3d}}\)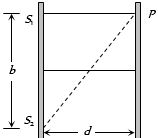
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionએક સ્લીટની વિવર્તન ભાતમાં કેન્દ્રીય શલાકાની પહોળાઈ ની સરખામણીમાં અન્ય શલાકાની પહોળાઈ.....
- 2યંગના પ્રયોગમાં બે સુસમ્બદ્ધ ઉદ્રગમો વચ્ચેનું અંતર $0.90\, mm $ છે અને પડદાનું ઉદગમોથી અંતર $1m$ છે. બીજી પ્રકાશિત શલાકાનુ મધ્યસ્થ પ્રકાશિત શલાકાના મધ્યબિદુથી અંતર $1\,mm $ હોય, તો વાપરેલ પ્રકાશની તરંગલંબાઈ શોધો.View Solution
- 3આપાતકોણ કે જ્યાં હવાથી કાચના વક્રીભવન (વક્રીભવનાંક) માટે પરાવર્તીંત પ્રકાશ સંપૂર્ણ ધ્રુવીભવન થાય છે. તે .......(વક્રીભવનાંક $n$)View Solution
- 4કાંચના સ્લેબ પર આપાત પ્રકાશનો આપાત કોણ $60^o$ છે, પરાવર્તીંત પ્રકાશ સંપૂર્ણ ધ્રુવીભૂત છે. કાંચની અંદર પ્રકાશના કિરણની ઝડપ ($ms^{-1}$ માં):View Solution
- 5$I$ અને $4 I$ તીવ્રતા ધરાવતા બે સુસંબધ્ધ એકરંગી પ્રકાશ કિરણપુંજ ને એકબીજા ઉપર સંપાત કરવામાં આવે છે. પરિણામી કિરણપુંજ ની મહતમ અને ન્યૂનતમ શક્ય તીવ્રતાઓ વચ્ચ્યેનો તફાવત $x \mathrm{I}$ છે. $x$ નું મૂલ્ય. . . . . . .થશે.View Solution
- 6View Solutionવ્યતિકરણમાં બે ઉદગમ કેવા હોવા જોઈએ.
- 7એક સ્લિટ દ્વારા મળતી વિવર્તન ભાતમાં. $6000$ $A$ તરંગલંબાઈ ધરાવતા પ્રકાશનો ઉપયોગ કરવામાં આવે છે. જ્યારે પડદાને સ્લિટ થી $50 \mathrm{~cm}$ જેટલો દૂર ખસેડવામાં આવે છે ત્યારે વિવર્તન ભાતમાં પ્રથમ અને તૃતીય લધુત્તમો વચ્ચેનું અતર $3 \mathrm{~mm}$ જેટલું મળે છે. સ્લિટની પહીળાઈ_________$\times 10^{-4} \mathrm{~m}$.View Solution
- 8જો $ y_1 = 4 \,sin \,\omega\, t$ અને $y_2 = \,3 \,sin \,( \omega \,t + \pi /3)$ વડે દર્શાવાતા બે તરંગો કોઈ એક બિંદુએ વ્યતિકરણ પામતાહોય તો પરિણામી તરંગનો કંપવિસ્તાર શોધો.View Solution
- 9View Solutionએક સ્લિટથી થતાં વિવર્તનમાં મધ્યસ્થ અધિકતમની નજીકની પ્રથમ ન્યુનતમ પર, સ્લિટની ધાર (એક છેડે) તથા તેના મધ્યમાં રહેલા બિંદુમાંથી ઉત્પન્ન થતી હાઇગેન્સ તરંગ અગ્રોની વચ્ચેનો કળા તફાવત કેટલો હશે?
- 10View Solutionવિવર્તનની ઘટના શેમાં જોવા મળે છે?
