Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1વિધાન : $B_2$ પરમાણુ પેરામેગ્નેટીક છે .View Solution
કારણ :સૌથી વધુ આણ્વિય કક્ષક સિગ્મા પ્રકારની છે. - 2View Solutionસમઇલેક્ટ્રોનિય જોડી કઈ છે?
- 3વિધાન : $SeCl_4$ ચતસ્ફલકીય બંધારણ નથી.View Solution
કારણ : $SeCl_4$ માં $Se$ ને બે એકલ જોડી છે. - 4વિધાન : ઓઝોન એ $O_2$ કરતાં વધારે પ્રબળ ઓક્સિડેશન કર્તા છેView Solution
કારણ : ઓઝોન ડાયમેગ્નેટીક છે અને $O_2$ પેરામેગ્નેટીક છે - 5વિધાન : $SF_4$ માંનો તમામ$F—S—F$ કોણ $90^o$ કરતા વધારે છે પરંતુ $180^o$ કરતા ઓછો છે,View Solution
કારણ : બંધ જોડી-બંધની જોડી અપાકર્ષણ કરતાં અબંધકારક જોડી-બંધની જોડીની અપાકર્ષણ નબળું છે. - 6વિધાન : $H_2O_2$ માં $O—O$ બંધની લંબાઈ $O_2F_2$ કરતા ટૂંકા હોય છે.View Solution
કારણ : $H_2O_2$ એ આયનીય સંયોજન છે - 7View Solutionનીચેના પરમાણુઓની કઇ વ્યવસ્થા તેમના દ્વિધ્રુવી ચાકમાત્રાના આધારે યોગ્ય છે?
- 8View Solutionનીચે પૈકી કયું સૌથી વધારે દ્વિધ્રુવીય ચાકમાત્રા ધરાવે છે?
- 9વિધાન : સિગ્મા $(\sigma )$ પ્રબળ બંધ છે , જ્યારે પાઇ $(\pi )$ એ નિર્બળ બંધ છેView Solution
કારણ : અણુઓ $(\pi )$ બંધ વિશે મુક્તપણે ફરે છે. - 10View Solutionનીચે પૈકી ક્યા અણુની ઉચ્ચ બંધ ઊર્જા ધરાવે છે?
- 11View Solutionનાનામાં નાનો બંધકોણ શેમાં જોવા મળે છે ?
- 12View Solutionનીચેનામાંથી કયું ધ્રુવીય સંયોજન છે ?
- 13View Solutionકાર્બન ડાયોક્સાઈડ માં કાર્બન ની પ્રથમ ,દ્વિતીય અને તૃતીય બંધ લંબાઈ શું હશે ?
- 14View Solutionનીચેનામાંથી કયું તત્વ નબળા આંતરઆણ્વિય બળોને પ્રદર્શિત કરે છે
- 15View Solutionફાજનના નિયમ મુજબ, સહસંયોજક બંધન કોના તરફેણ કરવામાં આવે છે ?
- 16વિધાન : પાણી પ્રવાહી છે પરંતુ $H_2S$ એ વાયુ છેView Solution
કારણ : ઑક્સીજન અનુચુંબકીય છે - 17View Solutionઈથેનોલ અને ડાયમિથાઈલ ઈથર ફંકશનલ આઈસોમર ની જોડી બનાવે છે. ઈથેનોલ નું ગલન બિંદુ ડાયમીથાઈલ ઈથર ની તુલના માં ઊંચું છે કારણ કે
- 18View Solutionશેમાં હાઈડ્રોજન બંધ હાજર નથી ?
- 19જ્યારે કાર્બન અણુની સંકરણ સ્થિતિ $s{p^3}$ થી $s{p^2}$ થી $sp,$ માં બદલાય છે, સંકર કક્ષક વચ્ચેનો કોણ શું હશે ?View Solution
- 20View Solutionનીચેનામાંથી કયા સંયોજન માં ધ્રુવીય અને અધ્રુવીય બંધ છે ?
- 21View Solutionનીચેનામાંથી કયું અનુચુંબકીય નથી ?
- 22View Solutionનીચેના સંયોજનોમાંથી, કયું સંયોજન રેખીય બંધારણ ધરાવે છે ?
- 23View Solutionપાણી ના ઊંચા ઉત્કલન બિંદુ નું કારણ શું છે?
- 24$\left[ {Cu\,{{\left( {N{H_3}} \right)}_4}} \right]\,S{O_4},\,\,;\,$ માં $Cu$ નું સંકરણ શું હશે ?View Solution
- 25In $HCHO,\,\,'C'$નું સંકરણ શું હશે ?View Solution
- 26જો બે પરમાણુ $A$ અને $B$ વચ્ચેના બંધ બનાવતી ઇલેક્ટ્રોન જોડી કેન્દ્રમાં નથી, તો તે બંધ કયો હશે ?View Solution
- 27View Solutionનીચેનામાંથી કયા ઘટકોમાં મહત્તમ સંખ્યામાં અબંધકારક ઇલેક્ટ્રોન છે ?
- 28View Solutionનીચેનામાંથી કયું વિધાન સાચું નથી ?
- 29View Solutionબંધ ક્રમાંક ...... માં મહત્તમ છે.
- 30View Solutionનીચેના માંથી ક્યાં સંયોજન માં ઈલેક્ટ્રોન ની ઉણપ જોવા મળે છે
- 31View Solutionપાણીના અણુમાં બંધકોણ લગભગ અથવા જળના નિર્દેશિત બંધનો કયો કોણ બનાવે છે
- 32કયો બંધ કોણ $\theta $ પરિણામે ત્રિઆણ્વિય અણુ $YXY$ માટે મહત્તમ દ્વિધ્રુવી ચાકમાત્રા પરિણમે છે ?View Solution
- 33View Solutionબંધ નો ક્રમ એ આણ્વીય કક્ષક સિદ્ધાંતમાં એક ખ્યાલ છે. તે બંધનિય અને અબંધનીય કક્ષકમાં ઇલેક્ટ્રોનની સંખ્યા પર આધારિત છે. નીચેનામાંથી કયું વિધાન તેના વિશે સાચું છે ?
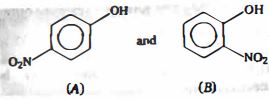
- 34ક્યો ખ્યાલ સારી રીતે સમજાવી શકે છે કે $o-$ નાઈટ્રોફિનોલ $p-$ નાઈટ્રોફિનોલ કરતા વધુ બાષ્પશીલ છે?View Solution
- 35View Solutionકયા પરમાણુઓ શૂન્ય દ્વિધ્રુવીય ક્ષણ ધરાવે છે
- 36ઓર્થો-નાઇટ્રોફિનોલ એ $p-$ અને $m-$ નાઇટ્રોફિનોલ્સ કરતાં પાણીમાં ઓછું દ્રાવ્ય છે કારણ કે:View Solution
- 37View Solutionનીચેનામાથી કોનુ બંધારણ સમતલીય સમચોરસ છે ?
- 38View Solutionશૂન્ય દ્વિધ્રુવીય ચાકમાત્રા સાથે ઝેનોન ધરાવતું સંયોજન કયું છે?
- 39જો કે $CN^-$ અને $N_2$ સમઇલેક્ટ્રોનીય છે, છતા $N_2$ અણુ... ને લીધે રાસાયણિક રીતે નિષ્ક્રિય છે.View Solution
- 40View Solutionનીચેનાં પૈકી સૌથી ટૂકો બંધ ધરાવતો ઘટક જણાવો.
- 41View Solutionનીચેનામાંથી કઇ જોડમાં બે ઘટકો સમબંધારણીય નથી ?
- 42નીતચેના ધટકો પૈકી ક્યા બે નો આકાર ત્રિકોણીય પિરામિડ છે?View Solution
$(I)$ $NI_3$ $(II)$ $I_3^-$
$(III)$ $SO_3^{-2}$ $(IV)$ $NO_3^-$
- 43$IF_7$ નું બંધારણ ............. છે.View Solution
- 44View Solutionનીચેનામાંથી ક્યુ સંયોજન સૌથી વધુ સહસંયોજક લાક્ષણિકતા દર્શાવે છે ?
- 45$MO$ સિદ્ધાંત પરથી અનુમાન કરો કે નીચેનામાંથી ક્યા ઘટકની બંધલંબાઇ સૌથી ઓછી છે ?View Solution
- 46View Solutionનીચેનામાંથી ક્યો ઘટક પ્રતિચુંબકીય ગુણ ધરાવે છે ?
- 47આવર્ત કોષ્ટકના સમૂહ$-15$માં $NH_3$ $(106^o )$ થી $SbH_3 \,\,(101^o )$ બંધકોણના ઘટતા મૂલ્યોનું કારણView Solution
- 48View Solutionનીચેનામાંથી ક્યા અણુ/આયનમાં બધા બંધ સમાન નથી.
- 49View Solutionનીચેનામાંથી ક્યો અણુ/આયન અયુગ્મિત ઇલેક્ટ્રોન ધરાવતો નથી ?
- 50$S{F_4},\,C{F_4}$ તથા $Xe{F_4}$ માં આણ્વિય આકાર ........ છે.View Solution
- 51View Solutionઆયનીય સંયોજનની લેટાઈસ ઊર્જા તેના પર નિર્ભર છે
- 52View Solutionનીચેનામાંથી ક્યા સેટમાં સમઈલેક્ટ્રોન ઘટકો નથી ?
- 53View Solutionનીચેનામાંથી ક્યો ઘટક પ્રતિચુંબકીય છે ?
- 54View Solutionકેલ્શિયમ કાર્બાઈડ માં બે કાર્બન પરમાણુઓ વચ્ચે બનતા બંધ નો પ્રકાર અને સંખ્યા શું હશે
- 55${H_2}S,N{H_3},B{F_2}$ અને $Si{H_4}$ માં બંધ ખૂણાનો સાચો ક્રમ (પ્રથમ નાનો પછી મોટો) નીચેનામાંથી ક્યો હશે?View Solution
- 56${H_2}S,N{H_3},B{F_3}$ અને $Si{H_4}$ માં બંધકોણનો સાચો ક્રમ ..........View Solution
- 57$NO$ નો બંધક્રમાંક $2.5$ છે જ્યારે $N{O^ + }$ નો બંધ ક્રમાંક $3$ છે. આ બે ઘટકો માટે નીચેનામાંથી ક્યું વિધાન સાચું છે?View Solution
- 58બંધકારક -બંધકારક ઇલેક્ટ્રોકયુગ્મો વચ્ચે $90^o$ ના ખૂણાની મહત્તમ સંખ્યા ....... માં છે.View Solution
- 59$NO$ નો બંધક્રમાંક $2.5$ છે, જ્યારે $N{O^ + }$ નો બંધક્રમાંક $3$ છે. આ બે ઘટકો માટે નીચેનામાંથી ક્યુ વિધાન સાચું છે?View Solution
- 60નીચેનામાંથી શામાં નિયમિત ચતુષ્ફલકીય બંધારણ છે?View Solution
(પરમાણ્વીય ક્રમાંક. : $B = 5,S = 16,Ni = 28,Xe = 54$)
- 61બોરિક એસિડ $({H_3}B{O_3})$ માં બોરોન અને ઓક્સિજન પરમાણુ માં ક્યુ સંકરણ બને છે.View Solution
- 62View Solutionકઇ પરમાણ્વિય કક્ષકોના સંકરણથી સમતલીય સમચોરસ સંકીર્ણ બને છે ?
- 63નીચેનામાંથી ક્યાં સમૂહમાં આંતરઆણ્વિય બંધકોણ ${109^o}28' $ છે ?View Solution
- 64View Solutionનીચેનામાથી ક્યુ વિધાન સત્ય છે ?
- 65$P_4O_{10}$ માં સિગ્મા બંધની સંખ્યા .......... છે.View Solution
- 66$AlF_3$નું ગલનબિંદુ $104\,^oC$ છે અને $SiF_4$નું ગલનબિંદુ $- 77\,^oC$ (તેનું ઊર્ધ્વપાતન થાય છે) કારણ કેView Solution
- 67$AX_2L_n$ પ્રકારનાં પરમાણુઓમાં (જ્યાં $L$ અબંધકારક ઇલેક્ટ્રોન યુગ્મનું પ્રતિનિધિત્વ કરે છે અને $n $ તેની સંખ્યા છે) ત્યાં $A$ અને $X$ તત્વ વચ્ચેનો બંધ અસ્તિત્વ ધરાવે છે.માટે $\angle X A X$ બંધકોણ એ ,...View Solution
- 68$BF_2NH_2$ પરમાણુ સંબંધિત ખોટું વિધાન ક્યું છે?View Solution
- 69$Cl - O$ બંધ ક્રમાંકનો સાચો ક્રમાંક કયો છેView Solution
- 70$HCl$ની દ્વિધ્રુવીય ચાકમાત્રા $1.03\, D$ છે, જો $H-Cl$ની બંધ લંબાઈ $1.26\,\overset{o}{\mathop{A}}\,,$ છે, તો $H-Cl$ બંધમાં આયનીય ગુણધર્મની ટકાવારી કેટલી ............. $\%$ છે ?View Solution
- 71$ICl$ અને $Br_2$નું પરમાણુ કદ લગભગ સમાન છે, પરંતુ $b .p.$ જો $ICl$ નું $Br_2$ કરતા આશરે $40\,^oC$ વધારે છે. તે કારણ છેView Solution
- 72$IF_5 , I_3^-$ અને $I^+_3$માં કેન્દ્રીય આયોડિન અણુનું સંકરણ અનુક્રમે છે,View Solution
- 73View Solutionકયા આયનીય સંયોજનમાં ઊર્જાનું મૂલ્ય સૌથી વધુ છે?
- 74કાર્બન ડાયોક્સાઇડ એ વાયુ છે, જ્યારે $SiO_2$ ઘન છે કારણ કેView Solution
- 75View Solution............ દ્વારા ઘન લેટાઈસમાં આયોડિન પરમાણુઓ રાખવામાં આવે છે.
- 76નીચે દર્શાવેલ બે સંયોજનોમાંથી, $B$ નું બાષ્પ દબાણ ચોક્કસ તાપમાને હોવાની અપેક્ષા છેView Solution
- 77View Solutionનીચેનામાંથી કયા ધાતુથી ધાતુ બંધ હાજર છે?
- 78નીચેનામાંથી કયા સંયોજનમાં દરેક શ્રેણીમાં અનુક્રમે સૌથી નાનો બંધકોણ $(X - A - X)$ છે?View Solution
$(A)\, OSF_2$ $OSCl_2$ $OSBr_2$
$(B)\, SbCl_3$ $SbBr_3$ $SbI_3$
$(C)\, PI_3$ $AsI_3$ $SbI_3$ - 79નીચેનામાંથી સંયોજનમાં $B-F$ બંધની લંબાઈ સૌથી ટૂંકી છે?View Solution
- 80નીચેના સંયોજનોમાંથી અષ્ટક બધા અણુઓ માટે સંપૂર્ણ અને અપૂર્ણ છેView Solution
$Al_2Cl_6$ $-$ $Al_2(CH_3)_6$ $-$ $AlF_3$ $-$ $BeCl_2$નો ડાઇમર $-$ $BeH_2$નો ડાઇમર
(Note : સંપૂર્ણ અષ્ટક માટે $C$ અને અપૂર્ણ અષ્ટક માટે $IC$)
- 81View Solutionનીચેની કઈ પ્રજાતિમાં ધ્રુવીય અને બિન-ધ્રુવીય બંધન છે પરંતુ સંપૂર્ણ અણુ ધ્રુવીય છે?
- 82વાતાવરણીય દબાણે $HF, H_2S, NH_3$ ના ઉત્કલન બિંદુનો ક્રમ નીચે પ્રમાણે ગોઠવી શકાય છે.View Solution
- 83$NH_3 , NH^+_4$ અને $NH^-_2$માં બંધ ખૂણાનો ક્રમ કયો છે?View Solution
- 84$NO^-_3 , AsO^{3-}_3 , CO^{2-}_3 , ClO^-_3 , SO^{2-}_3$ અને $BO^{2-}_3 $ની વચ્ચે બિન-સમતલીય ઘટકો ક્યાં છે?View Solution
- 85$O_2 F_2$ એક અસ્થાયી પીળો નારંગી ઘન છે અને $H_2O_2$ રંગહીન પ્રવાહી છે, બંનેમાં $H_2O_2$ અને $O_2F_2$માં $O-O$ બંધ અને $O-O$ બંધ લંબાઈ અનુક્રમે છે,View Solution
- 86$\overset{\bullet }{\mathop{C}}\,{{X}_{3}}$ સંયોજન વિષે ખોટું વિધાન કયું છે?View Solution
- 87$SF_4 , CF_4$ અને $XeF_4$ પરમાણુ વિશે સાચુ વિધાન કયું છે?View Solution
- 88$z-$ અક્ષને બંધ દિશા ધારીએ તો, બે અણુ $(A)$ અને $(B)$ ની આણ્વિય કક્ષાના સંમિશ્રણમાંથી કયા બંધનકર્તા બનશે?View Solution
$(I)\,$ $A$ની $s-$ કક્ષક અને $B$ની $P_x$ કક્ષક
$(II)\,$ $A$ની $s-$ કક્ષક અને $B$ની $P_z$ કક્ષક
$(Ill)\,$ $A$ની $p_y$ કક્ષક અને $B$ની $p_z$ કક્ષક
$(IV)\,$ $(A)$ અને $(B)$ની $s-$ કક્ષક
- 89અણુ $ML_x$માં $M$ એ ખાલી કક્ષકની આસપાસ ઇલેક્ટ્રોનની $7$ જોડીઓ સાથે સમતલમાં છે. $x$ની કિંમત છેView Solution
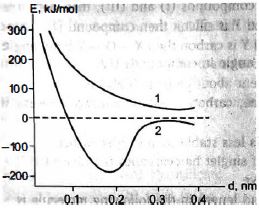
- 90આંતરઆણ્વિય અંતર વિરુદ્ધ સિસ્ટમની પોટેન્શિયલ ઊર્જા પર આધારીત $H^+_2$ આયનની રચના દર્શાવતા આપેલા આલેખને ધ્યાનમાં લો.View Solution
કયું વિધાન સાચું છે
- 91View Solutionઆપેલ ઘટકો વચ્ચેના પરમાણુ બળના આકર્ષણનો નીચેનામાંથી કયો ક્રમ ખોટો છે?
- 92View Solutionઉત્કલન બિંદુનો ખોટો ક્રમ કયો છે?
- 93એક પરમાણુ ઊર્જા ધરાવતા અનુક્રમે $E_1 , E_2$ અને $E_3$ એમ ત્રણ બંધારણ દ્વારા રજૂ થઈ શકે છે,આ બંધારણોની ઊર્જા અનુક્રમે. $E_3 < E_2 < E_1$ ક્રમનું પાલન કરે છે , જો પરમાણુની પ્રાયોગિક બંધ ઊર્જા $E_0$ છે, તો સંસ્પંદન ઊર્જા છે...View Solution
- 94View Solutionકયા સમૂહમાં ફક્ત સહ સંયોજક બંધવાળા પરમાણુઓ છે?
- 95View Solutionકયો પરમાણુ બિન-ધ્રુવીય તેમજ ધ્રુવીય બંધ ધરાવતું હોય છે પરંતુ સંપૂર્ણ અણુ ધ્રુવીય હોય છે
- 96View Solutionકેન્દ્રીય અણુનું સંકરણ બદલાશે જ્યારે
- 97ક્યા ઘટકમાં, $X-O$ બંધ ક્રમાંક $1.5$ છે અને તેમાં $p \pi - d \pi$ બંધ $(s)$શામેલ છે..View Solution
- 98જે ઘટકમાં $p \pi - p \pi$ બંધ નથી પરંતુ તેમાં $O_2$ના બંધ ક્રમાંક સાથે સમાન છેView Solution
- 99જો $P$ થી $T$નો બીજો સમયગાળો $p-$ સમૂહના તત્વો હોય તો પછી નીચેનો કયો ગ્રાફ $P_2$ થી $T_2$ (અનુરૂપ અણુઓ) માં સંયોજકતા ઇલેક્ટ્રોન વચ્ચે સાચો સંબંધ અને તેમનો બંધક્રમાંક બતાવે છેView Solution
- 100View Solutionનીચે આંતરઆણ્વિય અંતર ઘટવા પર, મહત્તમ અંતર (જ્યાં સંભવિત ઊર્જા લઘુત્તમ છે), ત્યાં સંભવિત ઊર્જામાં તીવ્ર વધારો છે