Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1View Solutionકયો પદાર્થ પ્રકાશીય સક્રિય નથી ?
- 2View Solutionકયો પ્રકાશીય સક્રિય અણુ છે ?
- 3View Solutionકયો મહત્તમ કેન્દ્રાનુરાગીતા ધરાવે છે ?
- 4View Solutionકાર્બનિક અણુ પ્રકાશ-ક્રિયાશીલતા ક્યારે દર્શાવે ?
- 5View Solutionકાર્બનિક અણુ પ્રકાશિય સક્રિયતા દર્શાવવા માટે શું જરૂરી છે ?
- 6View Solution....... કીરાલ સંયોજન છે.
- 7View Solutionજે પદાર્થ ધ્રુવીભૂત પ્રકાશના તળનું પરિભ્રમણ કરી શકે છે તેને કેવો પદાર્થ કહે છે ?
- 8View Solutionજે પદાર્થ ધ્રુવીભૂત પ્રકાશના તળનુ પરિભ્રમણ કરી શકે તેને........ કહે છે.
- 9View Solutionજે સમઘટકોના બંધારણ જુદા હોય અને એકબીજા સાથે સમતુલનમાં હોય તેને શું કહે છે ?
- 10View Solutionજે સમઘટકોના બંધારણો એકબીજાના બિનઅધ્યારોપણીય પ્રતિબિંબો હોય, તેને ..... કહે છે.
- 11View Solutionજે સમઘટકો પ્રકાશ ક્રિયાશીલ હોય પરંતુ એકબીજાના વસ્તુ પ્રતિબિંબ ન હોય તેવા પ્રકાશ સમઘટકો કયા નામે ઓળખાય છે ?
- 12View Solutionજો બે સંયોજન સમાન પ્રમાણ સૂચક સૂત્ર ધરાવતા હોય તથા આણ્વીય સૂત્ર જુદા હોય તો તે નીચેના પૈકી કયું ધરાવતા હોય ?
- 13$(+) -$ ટાર્ટરિક એસિડ અને મેસો ટાર્ટરિક એસિડએ ........View Solution
- 14ટ્રાન્સ $-2-$બ્યુટેનના બ્રોમિનેશન દ્વારા ઉદભવતાં પદાર્થના અવકાશીય સમઘટકોની સંખ્યા કેટલી છે ?View Solution
- 15View Solutionડાયઈથાઈલ ઈથર......નો મેટામર છે ?
- 16View Solutionડાયક્લોરો ઇથિલિન ............ દર્શાવી શકે નહિ
- 17View Solutionતે કિરાલ કેન્દ્ર ધરાવે છે. તો તે .....
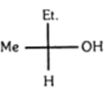
- 18View Solutionનીચેના પૈકી કયા પ્રતિબિંબીઓ છે ?
- 19View Solutionનીચેનામાંથી કઈ જોડી પ્રતિબિંબી વિન્યાસ સમઘટકતા દર્શાવે છે ?
- 20નીચેનામાંથી કયું અણુઓ જે અણુસૂત્ર $ C_4H_8O$ ધરાવે છે. જે પ્રકાશિય સમઘટકો દર્શાવે છે ?View Solution
- 21View Solutionનીચેનામાંથી કયું સંયોજન ભૌમિતિક સમઘટકતા દર્શાવતું નથી ?
- 22View Solutionનીચેનામાંથી કયું સંયોજન ભૌમિતિક સમઘટકતા દર્શાવતું નથી ?
- 23View Solutionનીચેનામાંથી કયો કેપિટલ અક્ષર એ કિરાલ છે ?
- 24View Solutionનીચેનામાંથી કયો સૌથી પ્રબળ બેઈઝ છે ?
- 25View Solutionનીચેનામાંથી કેન્દ્રાનુરાગી યોગશીલ માટે પ્રકાશક્રિયાશીલતાનો ક્રમ કયો છે ?
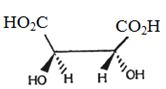
- 26View Solutionનો નિરપેક્ષ વિન્યાસ કયું છે ?
- 27View Solutionપરિભ્રમણ ધ્રુવીભૂત પ્રકાશનું માપન કોના દ્વારા થાય છે ?
- 28પેન્ટાઈન $ (C_5H_8)$ ના કેટલા સમઘટકો શક્ય છે ?View Solution
- 29View Solutionપ્રકાશ ક્રિયાશીલતા પરિમાપન માટે કયું સાધન વપરાય છે ?
- 30View Solutionપ્રકાશક્રિયાશીલતા ................. વડે માપવામાં આવે છે.
- 31View Solutionપ્રકાશીય સક્રિય સમઘટકો હોય પણ પ્રતિબિંબ ધરાવતા ન હોય તેને શું કહે છે ?
- 32View Solutionપ્રતિબિંબકારક ....... દ્વારા ઓળખી શકાતાં નથી.
- 33View Solutionપ્રતિબિંબિઓના અસ્તિત્વ માટે આવશ્યક અને પર્યાપ્ત શરત ........... છે.
- 34બને વ્ચ્ચે ક્યાં પ્રકાર ની સમઘટક્તા જોવા મળે છે ?View Solution
$C{H_3} - C{H_2} - C{H_2} - CN$ અને $C{H_3} - \mathop {CH}\limits_{\mathop |\limits_{CN} } \,\, - \,\,C{H_3}$
- 35બે પદાર્થો $\text{ }C{{H}_{3}}\,-\,\,C{{H}_{2}}\,-\,\,\overset{\overset{O}{\mathop{||}}\,}{\mathop{C}}\,\,\,-\,\,C{{H}_{2}}\,-\,\,C{{H}_{2}}\,-\,\,C{{H}_{3}}\,$ અને $C{{H}_{3}}\,-\,\,\overset{\overset{O}{\mathop{||}}\,}{\mathop{C}}\,\,\,-\,\,\overset{\overset{C{{H}_{3}}}{\mathop{|}}\,}{\mathop{\underset{\underset{C{{H}_{3}}}{\mathop{|}}\,}{\mathop{C}}\,}}\,\,\,-\,\,C{{H}_{3}}$ ને .......રીતે લઈ શકાય.View Solution
- 36View Solutionબ્યુટાઈલ આલ્કોહોલ અને આઈસો બ્યુટાઈલ આલ્કોહોલમાં કયા પ્રકારની સમઘટકતા જોવા મળે છે ?
- 37View Solutionભૌમિતિક અને પ્રકાશીય સમઘટકતા વચ્ચેની સમાનતા એ છે કે .....
- 38View Solutionભૌમિતિક સમઘટકો ....... માં અસમાનતા દર્શાવે છે ?
- 39View Solutionમેસો ટાર્ટરીક એસિડ કોની હાજરીના કારણે પ્રકાશીય નિષ્ક્રિય છે ?
- 40યુરિયા $\,\left[ {{H}_{2}}N\,\,-\,\,\underset{\underset{O}{\mathop{||}}\,}{\mathop{C}}\,\,\,-\,\,N{{H}_{2}} \right]$ અણુ કઈ (સમઘટક્તા) રીતે છે?View Solution
- 41રેસેમિક મિશ્રણ $d$ અને $l$ પ્રતિબિંબોમાં અલગીકરણની પદ્ધતિને ............. કહે છે.View Solution
- 42View Solutionરેસેમિક મિશ્રણનું પ્રકાશીય પરિભ્રમણ હંમેશા......
- 43રેસોમિક મિશ્રણને પ્રકાશીય શુદ્ધ $(+)$ અને $(-)$ પ્રતિબિંબકારકમાં અલગ કરવાની પદ્ધતિને શું કહે છે ?View Solution
- 44View Solutionશુદ્ધ ઈનાસ્યોમર્સ માં રેસેમિક મિશ્રણના વિભાજનને શાના તરીકે ઓળખવામાં આવે છે
- 45શુદ્ધ પ્રકાશીય પ્રતિબિંબકારકનું રૂપાંતરણ પ્રકાશીય નિષ્ક્રિય સમઆણ્વિય $(+)$ અને $(-)$ પ્રતિબિંબકારક મિશ્રણ થાય તેને શું કહે છે ?View Solution
- 46View Solutionસમઘટકોએ એકબંધની આસપાસ પરિભ્રમણ દ્વારા આંતર રૂપાંતર થાય છે તેને....
- 47View Solutionસમધટકોના ........... સમાન હોય છે.
- 48View Solutionસમાન અણુસૂત્ર પરંતુ જુદા જુદા બંધારણીય સૂત્રો ધરાવતા સંયોજનોને ........ કહે છે.
- 49View Solutionસમાનધર્મીઓ સમઘટકો હોઇ શકે ?
- 50View Solutionસામાન્ય પ્રકાર એ કોની મદદથી સમતલીય ધ્રુવીય પ્રકાશમાં રૂપાંતરણ પામે છે ?
- 51View Solutionસૌથી નાના બિન ચક્રિય હાઈડ્રો કાર્બન જે સીસ ટ્રાન્સ સમઘટકો દર્શાવવા માટે સક્ષમ હોય તેમાં હાજર કાર્બન પરમાણુઓની સંખ્યા કેટલી છે ?
- 52View Solutionહેકઝેનના પાંચ સમઘટકમાંથી કયો સમઘટક બે મોનોક્લોરીનેટેડ પદાર્થો આવે છે ?
- 53$2$ -બ્યુટોનોલ ના $4$ ગ્રામ અને $2$ - બ્યુટેનોલ ના $6$ ગ્રામ દ્રાવણ ને ઈનાસ્યોમેરિકની ગણતરી કરોView Solution
- 54$C_2H_3Cl_3$ અણુસૂત્ર ધરાવતા શક્ય સમઘટકોની સંખ્યા........... થશે.View Solution
- 55${C_2}{H_6}$ ના staggered conformation માં $H-C-H$ દ્રિતલીય ખૂણો ....$^o$ થશે.View Solution
- 56${C_3}{H_5}Cl$ અણસૂત્ર ધરાવતા શક્ય બંધારણીય સમઘટકોની સંખ્યા ............... થશે.View Solution
- 57${C_4}{H_{10}}O$ અણુસૂત્ર ધરાવતા બંધારણીય સમઘટકોની સંખ્યા કેટલી થશે ?View Solution
- 58${C_4}{H_{10}}O$ અણુસૂત્ર ધરાવતું સંયોજન ..... સમઘટકતા દર્શાવે.View Solution
- 59$C_4H_{10}O $ ના કેટલા બંધારણીય સમઘટકો શક્ય છે ?View Solution
- 60${C_4}{H_8}$ આણ્વિય સૂત્ર ધરાવતા શક્ય સમઘટકોની સંખ્યા .................. છે.View Solution
- 61${C_5}{H_{10}}$ ના કેટલા ચકીય સમઘટકો શક્ય છે ?View Solution
- 62${C_5}{H_{11}}OH$ અણુસૂત્ર ધરાવતા કેટલા સમઘટકો પ્રાથમિક આલ્કોહોલ થશે ?View Solution
- 63$C_6H_{12}O_6$ પરમાણુ સૂત્રનું સંયોજનમાં કેટલા દ્વિબંધ સમાન છે?View Solution
- 64$C_6H_{14}$ ના બંધારણીય સમઘટકોની સંખ્યા કેટલી છે ?View Solution
- 65${C_7}{H_8}O$ ના શક્ય સમઘટકોની સંખ્યા ......View Solution
- 66$C{H_3}CH = CH - CH = CH - CH = CH-Cl$ ના ભૌમિતિક સમઘટકોની સંખ્યા .............View Solution
- 67$C{H_3}CH\left( {COOH} \right) - CH\left( {COOH} \right) - C{H_2}C{H_3}$ સંયોજનના કેટલા પ્રકાશ સમઘટકો શક્ય છે ?View Solution
- 68$D$ -ગ્લિસરલડિહાઈડ નું બંધારણ કયું છે ?View Solution
- 69$E$ અને $Z$ નામકરણ મુજબ ક્યો સમઘટક $E$ છે ?View Solution
- 70$I$ અને $II$ એક બીજાના ભૌમિતિક સમઘટક છે કારણ કેView Solution
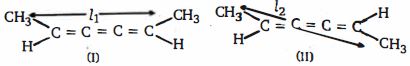
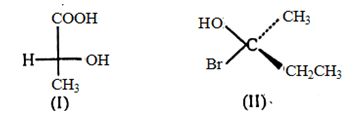
- 71$(i)$ અને $(ii)$ માટે અનુક્રમે કયા વિન્યાસ જોવા મળે છે ?View Solution
- 72${\left( {C{H_3}} \right)_2}CHC{H_2}C{H_3}$ ના ચાર મોનોક્લોરો વ્યુત્પન્નો મળે છે , જે પૈકી કેટલા પ્રકાશક્રિયાશીલ છે ?View Solution
- 73$(+)-$ Mandelic acid વિશિષ્ટ પરિભ્રમણ $+158^o$ છે. તો $25\%$ $(-)-$ Mandelic acid અને $75\%$ $(+)-$ Mandelic acid ના મિશ્રણનું વિશિષ્ટ પરિભ્રમણ .......$^o$ થશે ?View Solution
- 74$l_1$ અને $l_2$ ના વચેનો સાચો સંબંધ શું હશે ?View Solution
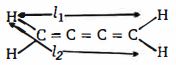
- 75ટ્રાંસ- $ 1, 4 $ - ડાયમિથાઇલસાયકલોહેકઝેન નું સ્થાયી સ્વરૂપ શેના તરીકે રજૂ થાય છેView Solution
- 76$Ph-CH = NO_2H \xrightarrow[{3days}]{{isomerises}}\mathop {(x)}\limits_{(50 - 50\% )}$ , સમઘટક $(x)$ શું હશે ?View Solution
- 77$R, S$ અગ્રતાના ક્રમમાં નીચેના જૂથોની ક્રમ આપો ($IV$ સૌથી વધુ છે)View Solution
$\mathop { - CH{{(C{H_3})}_2}}\limits_1 \,\,\,\,\,\,\,\,\,\,\,\mathop { - C{H_2}C{H_2}Br}\limits_2 \,\,\,\,\,\,\,\,\,\,\mathop { - C{H_2}Br}\limits_3 \,\,\,\,\,\,\,\,\,\,\mathop { - C{{(C{H_3})}_3}}\limits_4 $
$I = II = III = IV$
- 78$(S)-2$ ફ્લોરોબ્યુટનેનું કયું બંધારણ શ્રેષ્ઠ રજૂ કરે છેView Solution
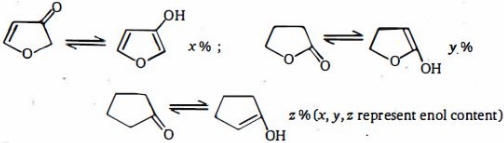
- 79$x, y, z$ નો સાચો ક્રમ કયો છે ?View Solution
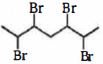
- 80અણુસૂત્ર $C_5H_{10} $ ના ચક્રિય પદાર્થોની કુલ સંખ્યા (અવકાશીય સમઘટકોને અવગણતા) કેટલી છે ?View Solution
- 81View Solutionઅપ્રતિબિંબો......... છે.
- 82અવકાશ રસાયણ ની જોડી વિવિધ રીતે વર્ગીકૃત કરવામાં આવી શકે છે. અવકાશ રસાયણ ની જોડીના સંદર્ભમાં નીચેનામાંથી કયું વિધાન સાચું છે?View Solution
$(a)$તેઓ વિન્યાસ સમઘટક હોઈ શકે છે $(b)$ તેઓ ડાયસ્ટીરિયોમર્સ છે
$(c)$તેઓ બંધારણીય સમઘટક હોઈ શકે છે $(d)$ તેઓ ટોટોમર્સ છે$(e)$ તેઓ સંરુપણ સમઘટક હોઈ શકે છે $(f)$ તેઓ ઈનાસ્યોમર્સ છે
$(g)$તેઓ સ્થાનીય સમઘટક છે - 83View Solutionઅવકાશસમઘટકની કઈ મહત્તમ સંખ્યા જે નીચેના સંયોજન માટે અસ્તિત્વમાં હોઈ શકે?
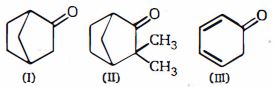
- 84આપેલ $(1), (2)$ અને $(3)$ સંયોજનોના સંદર્ભમાં કયું વિધાન સાચું છે ?View Solution

- 85View Solutionઆપેલ કીટોન્સમાં, કયું એક જે ઇનોલાઇઝ કરતું નથી
- 86View Solutionઆપેલ સંયોજન દ્વારા રચિત તમામ સંભવિત અવકાશીયસમઘટક ની સંખ્યા કેટલી છે
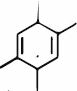
- 87View Solutionઆપેલ સંયોજનના ડાયસ્ટીરિયોમર્સ ની સંખ્યા કેટલી છે ?
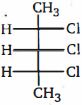
- 88View Solutionઆયોનિક ઘટકોને પ્રકિર્ણન (dispersal) પરિવર્તન દ્વારા સ્થિર કરી શકાય છે કયો કાર્બોક્સિલેટ આયન સૌથી સ્થિર છે ?
- 89View Solutionઆ સંયોજનનું સૌથી સ્થિર ખુરશીનું સ્વરૂપ કયું છે?
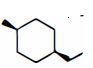
- 90ઇથાઇલ $-3-$ કિટો બ્યુટેનોએટ અને ઇથાઇલ $-૩-$ હાઇડ્રોક્સિ બ્યુટ્ $-2-$ ઇનોએટ એકબીજાના ................... થશે.View Solution
- 91View Solutionઇથિલિન ગ્લાયકોલનુ સૌથી સ્થાયી conformation ..... છે.
- 92ઉપરોક્ત જોડી માં $(A)$View Solution
અને $(B)$ વચે નો સંબંધ શું છે
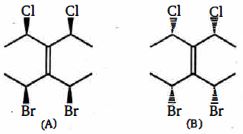
- 93ઉપરોક્ત સંયોજન માં $(A), (B), (C)$ અને $(D)$ ના કિરાલ સંયોજન કયું છેView Solution
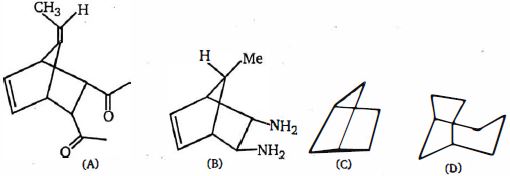
- 94View Solutionઉપરોક્ત સંયોજન માટે કેટલા ભૌમિતિક સમઘટક શક્ય છે?
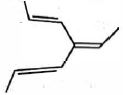
- 95View Solutionઉપરોક્ત સંયોજન માટે કેટલા ભૌમિતિક સમઘટક શક્ય છે?
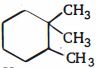
- 96એક હાઇડ્રોકાર્બનનુ આણ્વિય દળ $84$ ગ્રામ/મોલ છે, તો તેના આણ્વીય શૃંખલા સમઘટકોની સંખ્યા કેટલી થશે ?View Solution
- 97એક હાઇડ્રોકાર્બનનું આણ્વિય દળ $86$ ગ્રામ/મોલ છે, તો તેના શક્ય સમઘટકોની સંખ્યા કેટલી થશે ?View Solution
- 98એસિટોનની $D_2O $ સાથેની પ્રક્રિયા પછી તેનું ઈનોલ સ્વરૂપ ......View Solution
- 99View Solutionઓરડાના તાપમાને કયું સંતુલન ઝડપી નથી?
- 100View Solutionઓરડાના તાપમાને સમતલ ધ્રુવીકૃત પ્રકાશને નીચેના સંયોજનથી કયું સંયોજન ફેરવશે?