$1 \,\Omega$ તારની લંબાઈ $1\, m$ છે. તેની લંબાઈ $25\, \%$ વધે ત્યાં સુધી તેને તાણવામાં (ખેંચવામાં) આવે છે. નજીકતમ પૂર્ણાકમાં અવરોધમાં થતો પ્રતિશત ફેરફાર .....$\%$ છે.
JEE MAIN 2021, Diffcult
a
\(R _{0}=1\, \Omega\)
\(R _{0}=1\, \Omega\)
\(\ell_{0}=1\, m\)
\(A _{0}= A\)
\(R _{1}=?\)
\(\ell_{1}=1.25\, m\)
As volume of wire remains constant so
\(A _{0} \ell_{0}= A _{1} \ell_{1} \Rightarrow A _{1}=\frac{\ell_{0} A _{0}}{\ell_{1}}\)
Now
Resistance \(( R )=\frac{\rho \ell}{ A }\)
\(\frac{ R _{0}}{ R _{1}}=\frac{\ell_{0} / A _{0}}{\rho \ell_{1} / A _{1}}\)
\(\frac{1}{ R _{1}}=\frac{\ell_{0}}{ A _{0}}\left(\frac{\ell_{0} A _{0}}{\ell_{1} \times \ell_{1}}\right) R _{1}=\frac{\ell_{1}^{2}}{\ell_{0}^{2}}=1.5625\, \Omega\)
So \% change in resistance
\(=\frac{ R _{1}- R _{0}}{ R _{0}} \times 100\, \%\)
\(=\frac{1.5625-1}{1} \times 100 \,\%\)
\(=56.25\, \%\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક વાહકતારનો અવરોધ $50^{\circ} C$ તાપમાને $5$ ઓહમ અને $100^{\circ} C$ તાપમાને $6$ ઓહમ છે. તો $0^{\circ} C$ તાપમાને અવરોધ (ઓહમમાં) કેટલો હશે?View Solution
- 2એક મીટર લાંબા $Cu$-તારમાંથી $1 \,A$ નો પ્રવાહ વહે છે. જો તારના આડછેદનું ક્ષેત્રફળ $2.0\,mm ^{2}$ હોય અને $Cu$ ની અવરોધકતા $1.7 \times 10^{-8} \,\Omega m$ હોય તો તારમાં ગતિ કરતા ઈલેકટ્રોન દ્વારા અનુભવાતું બળ ............. $\times 10^{-23} \,N$ થશે.(charge on electorn $=1.6 \times 10^{-19} \,C$ )View Solution
- 3એક ઇલેકિટ્રક કીટલી ને $220\ V$ લગાડતાં તેમાંથી $4\ A$ પ્રવાહ વહે છે.આ કીટલીમાં ભરેલ $1\ kg $ પાણીને $20\,^o C$ થી ઊકળતા કેટલા ................ $min$ સમય લાગશે? પાણીનું ઉત્કલનબિદુ $100^o C$ છે.View Solution
- 4આપેલ પરિપથમાં રહેલા કેપેસિટર પર વિદ્યુતભાર ($nC$ માં) કેટલો હશે?View Solution
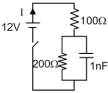
- 5આકૃતિમાં દર્શાવેલ નેટવર્કમાં $A B$ વચ્ચેનો અસરકારક અવરોધ $......... \Omega$View Solution
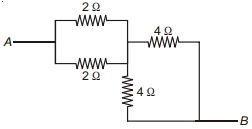
- 6આપેલ પરિપથમાં બધા અવરોધ $R$ ના છે. $A$ અને $B$ ટર્મિનલ વચ્ચેનો સમતુલ્ય અવરોધ કેટલો થાય?View Solution
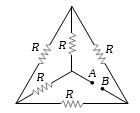
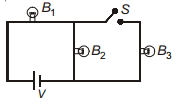
- 7ત્રણ એકસમાન બલ્બ $B_1, B_2$ અને $B_3$ ને આકૃતિમાં દર્શાવ્યા મુજબ મુખ્ય સપ્લાય સાથે. જોડેલ છે. જો $B_3$ એ કળ. $S$ બંધ કરીને પથમાંથી દૂર કરવામાં આાવે, તો બલ્બ $B_1$ ની ઉષ્ણતા કેટલી થશે?View Solution
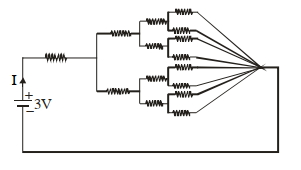
- 8આપેલ આકૃતિમાં દરેક અવરોધો $1 \,\Omega$ છે. પ્રવાહનું મૂલ્ય ' $I ^{\prime}, \frac{ a }{5} A$ જેટલું છે. $a$ નું મૂલ્ય .......... હશે.View Solution
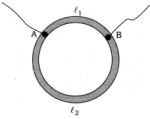
- 9એક તારનો અવરોધ $1$ મીટરદીઠ $12\,Ω$ છે.આ તારને $10\,cm $ ત્રિજયાવાળા વર્તુળાકારે વાળવામાં આવે છે. વર્તુળના વ્યાસાંતે આવેલાં બે બિંદુઓ $A$ અને $B$ વચ્ચેનો અવરોધ કેટલો થાય?View Solution

- 10એક રીંગ $R_0$ = $12\,\Omega$ અવરોધ ધરાવતા વાયરમાંથી બનાવેલ છે. તો $A$ અને $B$ બિંદુઓનું સ્થાન શોધો કે જેથી નીચે દર્શાવેલ પરીપથનો અવરોધ $8/3\,\Omega$ થી થાય.View Solution