\(P = 1 atm = 1 × 10^{5}N/m^{2}\)
\(T_1 = 27 + 273 = 300 K, T_2 = 627 + 273 = 900 K\)
સમોષ્મી ફેરફાર માટે, \(P^{1 -\gamma} T^{\gamma} =\) અચળ
\(\therefore \,\,\,{P_1}^{1 - \gamma }{T_1}^\gamma = {P_2}^{1 - \gamma }{T_2}^\gamma \,\,\,\,\,\therefore \,\,{\left( {\frac{{{P_2}}}{{{P_1}}}} \right)^{1 - \gamma }} = {\left( {\frac{{{T_1}}}{{{T_2}}}} \right)^\gamma }\)
\(\therefore \,\,\,{\left( {\frac{{{P_2}}}{{{P_1}}}} \right)^{\gamma - 1}} = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^\gamma }\,\,\,\,\,\,\,\therefore \,\,{\left( {\frac{{{P_2}}}{{{P_1}}}} \right)^{\frac{1}{2}}} = {\left( {\frac{{{T_2}}}{{{T_1}}}} \right)^{\frac{3}{2}}}\)
\(\therefore \,\,{\left( {\frac{{{P_2}}}{{{{10}^5}}}} \right)^{\frac{1}{2}}} = {\left( {\frac{{900}}{{300}}} \right)^{\frac{3}{2}}} = {(3)^{\frac{3}{2}}}\,\,\,\,\,\,\therefore \,\,\,\frac{{{P_2}}}{{{{10}^5}}} = {3^3}\)
\(\therefore \,\,\,{P_2} = 27 \times {10^5}N/{m^2}\)
Download our appand get started for free
Similar Questions
- 1પાણીના ઉત્કલનબિંદુ અને ઠારણબિંદુ વચ્યે કાર્યરત એન્જિનનીView Solution
$1$. કાર્યક્ષમતા $27 \%$ થતી વધારે હોય.
$2$. કાર્યક્ષમતા આ જ બે તાપમાનો વચ્ચે કાર્યરત કાર્નોટ એન્જિની કાર્યક્ષમતા કરતા ઓછી હોય.
$3$. કાર્યક્ષમતા $27 \%$ જેટલી હોય.
$4$. કાર્યક્ષમતા $27 \%$ કરતા ઓછી હોય.
નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
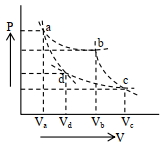
- 2આકૃતિમાં દર્શાવેલ $P-V$ આલેખમાં સમાન વાયુ માટે બે જુદા-જુદા સમોષ્મી પથો બે સમતાપીય વક્રોને છદે છે. $\frac{V_a}{V_d}$ ગુણોત્તર અને $\frac{V_s}{V_c}$ ગુણોત્તર વચ્ચેનો સંબંધ. . . . . . . છે.View Solution
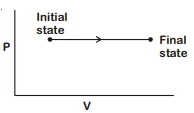
- 3અચળ દબાણ $P$ એ વાયુનું કદ $ {V_1} $ થી વધારીને $ {V_2} $ કરવામાં આવે છે.તો વાયુ પર થતું કાર્ય?View Solution
- 4રેફીજરેટરના બહારના ભાગનું અને અંદરના ભાગનું તાપમાન અનુક્રમે $273 \,K$ અને $300 \,K$ છે. ધારો કે રેફ્રીજેરટરનું યક્ર પ્રતિવર્તી છે, થયેલ કાર્યની દરેક જૂલ માટે, પરિસરમાં આપવામાં આવતી ઉષ્મા લગભગ ......... $J$ હશે.View Solution
- 5થર્મોોડાયનેમિક પ્રક્રિયા હેઠળની પિસ્ટન સિલિન્ડર એસેમ્બલીમાં આદર્શ ગેસ માટેનો $P - V$ ગ્રાફ ................. પ્રક્રિયા દર્શાવે છેView Solution
- 6View Solutionથરર્મોડાયનેમિક પ્રક્રિયા માટે કયું વિધાન ખોટું છે.?
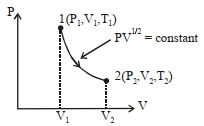
- 7$1$ મોલ આદર્શ વાયુ માટે, ઉષ્માગતિશાસ્ત્ર પ્રક્રિયાને $P-V$ આકૃતિ દ્વારા દર્શાવવામાં આવેલ છે. જે $V _{2}=2 V _{1}$ હોય તો તાપમાનનો ગુણોત્તર $T _{2} / T _{1}$ ........ છે.View Solution
- 8એક આદર્શ રેફ્રિજરેટરના ફ્રીઝર વિભાગનું તાપમાન $-13 °C$ છે. જો રેફ્રિજરેટરનો પરફોર્મન્સ ગુણાંક $5$ હોય, તો વાતાવરણનું તાપમાન (વાતાવરણ કે જ્યાં ઉષ્મા ગુમાવવામાં આવે છે.) = ......View Solution
- 9$2\, mol$ વાયુને સમોષ્મી વિસ્તરણ કરાવતાં આંતરિક ઊર્જા $100\, J$ ધટે છે.તો વાયુ દ્વારા ..... $J$ કાર્ય થશે.View Solution
- 10સમોષ્મી પ્રક્રિયામાં $1 \,\,mol$ આદર્શ વાયુનું પ્રારંભિક અને અંતિમ તાપમાન અનુક્રમે $T_1$ અને $T_2$ છે, તો વાયુની આંતરિક ઊર્જામાં થતો ફેરફાર .......View Solution
