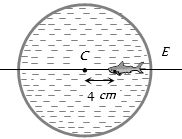
$10\, cm $ ત્રિજ્યાના ગોળાકાર પાત્રને $(4/3)$ વક્રીભવનાંક વાળા પાણીથી ભરેલું છે. આકૃતિમાં બતાવ્યા પ્રમાણે કેન્દ્ર $C$ થી $4 \,cm$ ના અંતરે એક માછલી છે. જો છેડા $E$ થી જોવામાં આવે તો માછલી ......$cm$ દેખાતી હશે? (માછલી જોડાઈ અવગણતાં)
Medium
Download our app for free and get started
a
(a) By using \(\frac{{{\mu _2}}}{v} - \frac{{{\mu _1}}}{u} = \frac{{{\mu _2} - {\mu _1}}}{R}\)
where \({\mu _1} = \frac{4}{3},\) \({\mu _2} = 1,\) \(u = - 6\,cm,\) \(v = ?\)
On putting values \(v = - 5.2\,cm\)
(a) By using \(\frac{{{\mu _2}}}{v} - \frac{{{\mu _1}}}{u} = \frac{{{\mu _2} - {\mu _1}}}{R}\)
where \({\mu _1} = \frac{4}{3},\) \({\mu _2} = 1,\) \(u = - 6\,cm,\) \(v = ?\)
On putting values \(v = - 5.2\,cm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$15\, cm$ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાથી રચાતા પ્રતિબિંબનું રેખીય પરિમાણ તે પદાર્થથી બમણું છે. જો પ્રતિબિંબ આભાસી હોયતો પદાર્થનું સ્થાન ......$cm$ હશે.View Solution
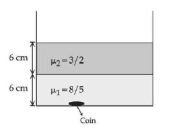
- 2મિશ્રિત ન થઈ શકે તેવા અનુકમે $\frac{8}{5}$ અને $\frac{3}{2}$ વકીભવનાંક ધરાવતા બે પ્રવાહીને આક્રૂતિમાં દર્શાવ્યા મુજબ રાખવામાં આવેલ છે. પ્રત્યેક પ્રવાહી સ્થંભની ઉંચાઈ $6 \mathrm{~cm}$ છે. બીકરના તળિયે એક સિક્કો મૂકેલો છે. નજીકતમ દષ્ટિ અંતર માટે, સિક્કાની આભાસી ઉંડાઈ $\frac{\alpha}{4} \mathrm{~cm}$ છે. $\alpha$ નું મૂલ્ય_______છે.View Solution
- 3એક ટાંકી $12.5\,cm$ ઉંચાઈ સુધી પાણીથી ભરેલી છે. ટાંકીને નીચેની સપાટી પર પડેલી સોયની આભાસી ઉડાઈ માઈક્રોસ્કોપ વડે માપવામાં આવતાં $9.4 \,cm$ મળે છે. તો પાણીનો વક્રીભવનાંક ..... હશે.View Solution
- 4$20 \,cm$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સને બે સમાન ભાગમાં કાપવામાં આવે છે. તેથી તેના આકૃતિમાં દર્શાવ્યા મુજબ બે સમતલીય બહિર્ગોળ લેન્સ બને છે. ત્યારબાદ આ બંન્ને ભાગને આકૃતિમાં દર્શાવ્યા મુજબ એકબીજાના સંપર્કમાં મૂકવામાં આવે છે. તો તંત્રની કેન્દ્રલંબાઈ .......$cm$ થશે?View Solution
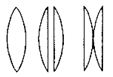
- 5એક વ્યકિતનું નજીકનું બિંદુ $60\;cm $ છે. આંખથી $2\;cm$ દૂર રહેલા ચશ્માના ગ્લાસથી, $22\;cm$ દૂર વાંચવા માટેના ચશ્માના કાંચની કેન્દ્રલંબાઇ ($cm$ માં) કેટલી હશે?View Solution
- 6સાદા માઇક્રોસ્કોપમાં $2.5 cm$ કેન્દ્રલંબાઇ ધરાવતો બર્હિગોળ લેન્સ વાપરતાં તેની મહતમ મોટવશક્તિ કેટલી થાય? (સ્પષ્ટ દ્રષ્ટિ માટે ન્યૂનતમ અંતર $25\, cm$)View Solution
- 7$μ_1$, $μ_2$, $μ_3$ અને $μ_4$ વક્રીભવનાંક ધરાવતા માધ્યમમાંથી પસાર થતા કિરણનો માર્ગ આપેલ છે. બધા માધ્યમની સપાટી સમાંતર છે. નિર્ગમન કિરણ $CD$ એ આપાત કિરણ $AB$ સમાંતર છે તો...View Solution
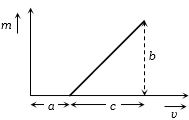
- 8બર્હિગોળ લેન્સ માટે મોટવણી $(m)$ અને પ્રતિબિંબ અંતર $(v)$ નો આલેખ આપેલ છે,તો તેની કેન્દ્રલંબાઇ કેટલી હશે?View Solution
- 9પાતળા સમબહિર્ગોળ લેન્સની ઓપ્ટિક અક્ષ $x - $ અક્ષ છે. વસ્તુના અને તેના પ્રતિબિંબના સ્થાનના યામ અનુક્રમે $ (-40\,\, cm , 1\,\, cm)$ અને $(50\,\, cm, - 2 \,\,cm )$ છે, તો લેન્સનું સ્થાન શું થશે ?View Solution
- 10એક દાઢી કરવાનો અરીસો માણસ તેનાથી $10\,cm$ અંતરે મૂકે છે અને તે પોતાનું પ્રતિબિંબ નજીકતમ અંતર $25\,cm$ અંતરે જોવે છે તો આ અરિસાની વક્રતાત્રિજ્યા કેટલા $cm$ હશે?View Solution