Base area of the given \(\operatorname{tank}, A=1.0 m ^{2}\)
Area of the hinged door, \(a=20 cm ^{2}=20 \times 10^{-4} m ^{2}\)
Density of water, \(\rho_{1}=10^{3} kg / m ^{3}\)
Density of acid, \(\rho_{2}=1.7 \times 10^{3} kg / m ^{3}\)
Height of the water column, \(h_{1}=4 m\)
Height of the acid column, \(h_{2}=4 m\)
Acceleration due to gravity, \(g=9.8\)
Pressure due to water is given as:
\(P_{1}=h_{1} \rho_{1} g\)
\(=4 \times 10^{3} \times 9.8\)
\(=3.92 \times 10^{4} Pa\)
Pressure due to acid is given as:
\(P_{2}=h_{2} \rho_{2} g\)
\(=4 \times 1.7 \times 10^{3} \times 9.8\)
\(=6.664 \times 10^{4} Pa\)
Pressure difference between the water and acid columns:
\(\Delta P=P_{2}-P_{1}\)
\(=6.664 \times 10^{4}-3.92 \times 10^{4}\)
\(=2.744 \times 10^{4} Pa\)
Hence, the force exerted on the door \(=\Delta P \times a\) \(=2.744 \times 10^{4} \times 20 \times 10^{-4}\)
\(=54.88 N\)
Therefore, the force necessary to keep the door closed is \(54.88 \;N .\)
Download our appand get started for free
Similar Questions
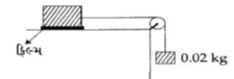
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે જેના પાયાનું ક્ષેત્રફળ $0.2 \;m^2$ હોય, તેવા એક બ્લેાકને $0.02 \;kg$ નું દળ એક દોરી વડે એક આદર્શ ગરગડી પરથી લગાડેલ છે. એક પ્રવાહીનું $0.6\; mm$ જાડાઈનું પાતળું સ્તર આ બ્લોક અને ટેબલ વચ્ચે મૂકવામાં આવે છે. જયારે બ્લોકને છોડવામાં આવે ત્યારે તે $0.17 \;m/s$ ની અચળ ઝડપથી જમણી તરફ ગતિ કરે છે. આ પ્રવાહીનો સ્નિગ્ધતાંક કેટલો હશે?View Solution
- 2$6\,mm$ વ્યાસ ધરાવતો એક હવાનો પરપોટો $1750\,kg / m ^3$ ની ધનતા ધરાવતા દ્વાવણમાંથી $0.35\,cm / s$. ના દરે એકધારી રીતે ઉપર તરફ જાય છે. દ્રાવણનો સ્નિગધતા અંક (હવાની ધનતાને અવગણતા) $......Pas$ છે. ($g =10\,m / s ^2$ or $ms ^{-2}$ આપેલ છે.)View Solution
- 3$5\, cm$ ત્રિજ્યા ધરાવતી પાઇપમાથી પાણી $100\,$ લિટર પ્રતિ મિનિટ ના દરથી આવે તો પ્રવાહનો રેનોલ્ડ નંબર કયા ક્રમનો હશે? (પાણીની ઘનતા $= 1000\, kg/m^3$, પાણીનો શ્યાનતાગુણાંક $= 1\, mPa\, s$)View Solution
- 4View Solutionપાઇપમાં પ્રવાહીનું વહન ધારારેખી કરવા માટે
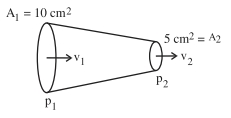
- 5$1.25 \times 10^3\,kg\,m ^{-3}$ ધનતા ધરાવતું ગ્લિસરીન પાઈપના શંકુ વિભાગમાંથી વહન પામે છે. નળીના છેડાના આડછેદના ક્ષેત્રફળ $10\,cm ^2$ અને $5\,cm ^2$ તેમજ તેની લંબાઈ દરમિયાન દબાણનો ધટાડો $3\,Nm ^{-2}$ છે. નળીમાંથી થતો ગ્લિસરીનનો વહનનો દર $x \times 10^{-5}\,m ^3\,s ^{-1} છ$. તો $x$ નું મૂલ્ય $.......$ છે.View Solution
- 6ત્રાજવામાં મૂકેલા બે પદાર્થો પાણીમાં સમતોલનમાં રહે છે,એક પદાર્થનું દળ $36 g$ અને ઘનતા $9 \,g / cm^{3}$છે,જો બીજા પદાર્થનું દળ $48 \,g$ હોય,તો તેની ઘનતા ..... $g / cm^{3}$ હશે.View Solution
- 7$A $ અને $B $ પદાર્થો પાણીમાં તરે છે,$A$ પદાર્થનું $\frac{1}{2}$ કદ પાણીમાં ડુબેલું અને $B $ પદાર્થનું $\frac{1}{4}$કદ પાણીની બહાર છે,તો ઘનતાનો ગુણોત્તર કેટલો થાય?View Solution
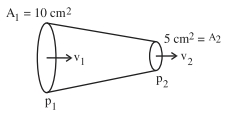
- 8$1.25 \times 10^3\,kg\,m ^{-3}$ ધનતા ધરાવતું ગ્લિસરીન પાઈપના શંકુ વિભાગમાંથી વહન પામે છે. નળીના છેડાના આડછેદના ક્ષેત્રફળ $10\,cm ^2$ અને $5\,cm ^2$ તેમજ તેની લંબાઈ દરમિયાન દબાણનો ધટાડો $3\,Nm ^{-2}$ છે. નળીમાંથી થતો ગ્લિસરીનનો વહનનો દર $x \times 10^{-5}\,m ^3\,s ^{-1} છ$. તો $x$ નું મૂલ્ય $.......$ છે.View Solution
- 9$40\; m/s $ ની ઝડપથી ઘરમાં છતને સમાંતર પવન ફૂંકાય છે. છતનું ક્ષેત્રફળ $250 \;m^2$ છે. ઘરમાં દબાણ, વાતાવરણના દબાણ જેટલું ધારીએ તો છત પર પવન દ્વારા લાગતું બળ અને તેની દિશા શું હશે? ($\rho _{air} $ $=1.2 \;kg/m^3$)View Solution
- 10નળમાથી પાણી નીચે તરફ $1.0\,ms^{-1}$ ના વેગથી નીકળે છે.નળના આડછેદનું ક્ષેત્રફળ $10^{-4}\,m^2$ છે. પાણીમાં દરેક જગ્યાએ દબાણ સમાન છે અને પ્રવાહ ધારારેખી છે.નળથી $0.15\,m$ નીચે પ્રવાહના આડછેદનું ક્ષેત્રફળ કેટલું હશે? ($g = 10\,ms^{-2}$ )View Solution
