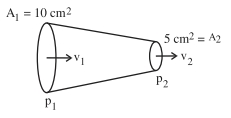
\(\Delta P = P _1- P _2=3 N / m ^2 \text { (given) }\)
By continuity \(eq ^{ n }\)
\(A _1 v _1= A _2 v _2\)
\(\therefore \quad v_1=\frac{A_2}{A_1} v_2-(1)\)
By Bernoulli's equation.
\(P _1+\frac{1}{2} \rho v _1{ }^2= P _2+\frac{1}{2} \rho v _2{ }^2\)
\(P _1- P _2=\frac{1}{2} \rho\left( v _2^2- v _1^2\right)\)
\(\Delta P =\frac{1}{2} \rho\left( v _2^2-\frac{ A _2^2}{ A _1^2} v _2^2\right)\)
\(\Delta P =\frac{1}{2} \rho\left[1-\left(\frac{ A _2}{ A _1}\right)^2\right] v _2^2\)
\(3=\frac{1}{2} \times 1.25 \times 10^3\left[1-\left(\frac{5}{10}\right)^2\right] v _2^2\)
\(3=\frac{1}{2} \times 1.25 \times 10^3\left[1-\frac{1}{4}\right] v _2^2\)
\(3=\frac{1}{2} \times 1.25 \times 10^3 \times \frac{3}{4} v_2^2\)
So discharge rate \(= A _2 V _2\)
\(=5 \times 10^{-4} \times 8 \times 10^{-2}\)
\(=4 \times 10^{-5}\,m ^3 / s\)
Correct ans is \(x=4\)
Download our appand get started for free
Similar Questions
- 1${\rho _1}$ અને ${\rho _2}$ ધનતા અને સમાન કદ ઘરાવતી બે ઘાતુનું મિશ્રણ કરવાથી મિશ્રણની સાપેક્ષ ઘનતા $4$ છે.આ બે ઘાતુનુ સમાન દળ લઇને મિશ્રણ કરવાથી મિશ્રણની સાપેક્ષ ઘનતા $3$ છે. તો ${\rho _1}$ અને ${\rho _2}$ કેટલા થાય?View Solution
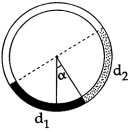
- 2એક વર્તુળાકાર નળી ઊર્ધ્વ સમતલમાં રાખેલ છે.બે પ્રવાહી કે જેઓ એકબીજામાં ભળી શકતા નથી અને તેમની ધનતા $d_1$ અને $d_2$ છે.તેમને આ નળીમાં ભરવામાં આવે છે.દરેક પ્રવાહી કેન્દ્ર આગળ $90°$ નો આંતરિક કોણ રચે છે.જયારે આંતર સપાટીને જોડતી ત્રિજયા શિરોલંબ સાથે $\alpha $ કોણ રચે છે,તો ગુણોત્તર $\frac{{{d_1}}}{{{d_2}}}$View Solution
- 3બે મોટા હાડકાના આડછેદના ક્ષેત્રફળ $10 \,cm ^2$ છે અને ઉપરનો ભાગ $50 \,kg$. ધરાવતા વ્યક્તિના ઉપરના ભાગ સાથે જોડેલ છે. તો સરેરાશ હાડકા વડે થતું દબાણ ............ $N / m ^2$View Solution
- 4વિધાન : $Re > 2000$ માટે પ્રવાહ પ્રક્ષુબ્ધ હોયView Solution
કારણ : વધુ રેનોલ્ડ નંબર માટે જડત્વિય બળો શ્યાનતાબળો કરતાં વધુ પ્રભાવી હોય
- 5સ્નિગ્ધ પ્રવાહીમાં પદાર્થ જ્યારે શિરોલંબ રીતે પડતો હોય ત્યારે તેના પર બળ $F = -kv$ ($k$ અચળાંક છે) લાગે તો તેના માટે વેગ $v$ અને પ્રવેગ $a$ માટેનો સાચો ગ્રાફ નીચેનામાથી કયો થશે?View Solution
- 6$1\, cm^2$ ક્ષેત્રફળ ધરાવતી સપાટી પર $1\,gm$ દળના $10000$ દડાને, દર સેકન્ડે $100\, m/s$ ના વેગથી અથડાવવામાં આવે છે.અ દડાઓ સમાન વેગથી પાછા ફરતા હોય,તો સપાટી પર કેટલું દબાણ લાગતું હશે?View Solution
- 7બે કોપરના પાત્ર $A$ અને $B$ સમાન પાયાનું ક્ષેત્રફળ પરંતુ અલગ આકાર ધરાવે છે. એક ચોક્કસ સામાન્ય ઊંચાઈ સુધી પાણી ભરતા $A$ દ્વારા રોકતું કદ $B$ કરતાં બમણું મળે છે. તો નીચેનામાંથી સાચું વિધાન કયું છે?View Solution
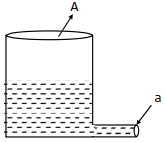
- 8એક હલકા નળાકારીય સમક્ષિતિજ સપાટી ઉપર રાખવામા આવેલ છે. તેના તળિયાનો આડછેદ $A$ છે. તેના તળિયા આગળ $a$ જેટલું આડછેદનું ક્ષેત્રફળ ધરાવતું એક છિદ્ર બનાવવામાં આવે છે. બહાર નીકળતા પ્રવાહીને કારણે લાગતાં બળને કારણે પાત્રને ન ખસેડવા માટે જરૂરી લઘુતમ ઘર્ષણાંક ............ હશે. $(a\,<\,<\,A)$View Solution
- 9$20\; m$ ની ઊંચાઈનો નળાકાર સંપૂર્ણપણે પાણીથી ભરેલો છે. તેના તળિયાની નજીક નળાકારની બાજુની દિવાલ પરના નાના છિદ્રમાંથી બહાર આવતા પાણીના પ્રવાહનો વેગ ($ m/s$ માં) કેટલો હશે?View Solution
- 10એક નાનો $m$ દળ અને $\rho$ ધનતા ધરાવતા બોલને $\rho_0$ જેટલી ધનતા ધરાવતા સિન્ગધ પ્રવાહીમાં મૂકવામાં આવે છે. અમુક સમયબાદ, બોલ અચળ વેગ સાથે પડે છે. બોલ ઉપર લાગતું સ્નિગધ (શ્યાનતા) બળ . . . .હશે.View Solution
