$1.0\ mm^2$ ક્ષેત્રફળ વાળા કોપર તારના આડછેદમાં $1.34\ A$ પ્રવાહ મળે છે. ધારો કે દરેક કોપરનો પરમાણું એક મુક્ત ઈલેકટ્રોન આપે છે. તો તારમાં મુક્ત ઈલેકટ્રોનની ડ્રિફટ ઝડપની ગણતરી ................... $mm/s$ કરો, કોપરની ઘનતા $8990\ kg/m^3$ અને પરમાણવીય દળ = $63.50$
Medium
c
કોપરના \(1\ m^3\) કદનું દળ = \(8990\ kg = 8990 \times 10^3\ g\)
કોપરના \(1\ m^3\) કદનું દળ = \(8990\ kg = 8990 \times 10^3\ g\)
\(\,1 \,{m^3} \) માં મોલની સંખ્યા \( = \,\,\frac{{8990\,\, \times \,\,1{0^3}}}{{63.5}}\,\, = \,\,1.4\,\, \times \,\,{10^5}\)
જ્યાં સુધી દરેક મોલ \(6 \times 10^{23}\) પરમાણુ ધરાવે છે તેથી \(\,1\, {m^3} \) માં અણુઓની સંખ્યા
\(n = (1.4 \times 10^5) \times (6 \times 10^{23}) = 8.4 \times 10^{28}\)
\(i = neAv_d\)
\({v_d}\,\, = \,\,\frac{i}{{neA}}\)
\( = \,\,\frac{{1.34}}{{8.4\,\, \times \,\,{{10}^{28}}\,\, \times \,\,1.6\,\, \times \,\,{{10}^{ - 19}}\,\, \times \,\,{{10}^{ - 6}}}}\)
\(\left( {\,\because \,\,\,1\,\,m{m^2}\,\, = \,\,{{10}^{ - 6}}\,\,{m^2}\,} \right)\)
\( = \,\,{10^{ - 4}}\,\,m/s\,\, = \,\,0.1\,\,mm/s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક બેટરીને બીજી $15\,V$ બેટરી વડે $8 $ કલાક ચાર્જ કરતાં $10\,A$ પ્રવાહ વહે છે. આ બેટરી જયારે ડિસ્ચાર્જ થાય છે,ત્યારે $5\,A$ નો પ્રવાહ $15$ કલાક સુધી વહે છે.ડિસ્ચાર્જ સમયે તેનો સરેરાશ ટર્મિનલ વોલ્ટેજ $ 14\,V$ રહે છે.આ બેટરીની $watt\, hour $ કાર્યક્ષમતા કેટલા $\%$ હશે?View Solution
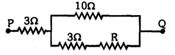
- 2અહિં દર્શાવેલ પરિપથમાં અજ્ઞાત અવરોધ $R$ નું મૂલ્ય શું હશે કે જેથી બિંદુઓ $'P'$ અને $'Q'$ વચ્ચેનો કુલ અવરોધ પણ $R$ જેટલો જ હોય.View Solution
- 3બે બલ્બો જેમના અવરોધો $1 : 2$ ગુણોત્તરમાં છે. તેઓને અચળ વોલ્ટેજના ઉદગમ સાથે સમાંતરમાં જોડેલ છે. તો જોડાણમાં પાવર વ્યયનો ગુણોત્તર કેટલો હશે ?View Solution
- 4બ્રાઉન,કાળો અને બ્રાઉન કલર ધરાવતા કાર્બનના અવરોધનું મૂલ્ય કેટલા ............ $\Omega$ થાય?View Solution
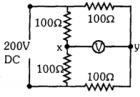
- 5નીચેના પરિપથ માટે $x$ અને $y$ વચ્ચેનો સ્થિતિમાનનો તફાવત .........છે.View Solution
- 6એક અવરોધક તારનો અવરોધ $50\,^o$ સે તાપમાને $5\,\Omega$ અને $100\,^o$ સે તાપમાને $6\,\Omega$ છે. તો $0\,^o$ સે તાપમાને તેનો અવરોધ .............. $\Omega$ હશે.View Solution
- 7ઇલેક્ટ્રીક કીટલીને ચાલુ કર્યા બાદ $15\,\min$ માં પાણી ઉકળવા લાગે છે. હીટીંગ વાયરની લંબાઈ તેની મૂળ લંબાઈ કરતા $2/3$ ગણી કરવામાં આવે તો સમાન પાણીના જથ્થાને ગરમ થતા લાગતો સમય ........... $min$View Solution
- 8પ્રવાહ પસાર થતાં વાહકનું તાપમાન $5\,^oC$ વધે છે. જ્યારે પ્રવાહ બમણો કરવામાં આવે ત્યારે તો તેમાં તાપમાનનો કેટલા $^oC$ નો વધારો થાય?View Solution
- 9મીટર બ્રિજની ડાબી બાજુના છેડાથી સંતુલન લંબાઈ $20$ સેમી છે (જમણી બાજુના ખાંચામાં પ્રમાણભૂત અવરોધ $1\,\Omega$ છે) અજ્ઞાત અવરોધનું મૂલ્ય ($\Omega$ માં) કેટલું હશે?View Solution
- 10$200\, {W},\;100 \,{V}$ ના રેટિંગ ધરાવતા બલ્બને $200\, {V}$ ના ઉદગમ સાથે જોડેલ છે. કેટલા મૂલ્યના ($\Omega$ માં) $R$ અવરોધને તેની સાથે શ્રેણીમાં જોડાવો જોઈએ કે જેથી બલ્બ સમાન પાવર આપે?View Solution
