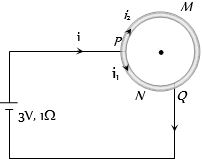
આકૃતિમાં દર્શાવ્યા મુજબ \({\text{PQR}}\) ભાગનો અવરોધ \({R_1} = \frac{{10}}{4} = 2.5\,\Omega \,\,\)
અને \(\,{\text{PMQ}}\) ભાગનો અવરોધ \( \Rightarrow {\text{ }}{R_2} = \frac{3}{4} \times 10 = 7.5\,\Omega \)
\({R_{eq}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{2.5 \times 7.5}}{{(2.5 + 7.5)}}\,\, = \,\,\frac{{15}}{8}\,\Omega \)
મુખ્ય પ્રવાહ \(i\,\,\, = \,\,\,\,\frac{3}{{\frac{{15}}{8} + 1}} = \frac{{24}}{{23}}\,A\,\,\,\)
\( \Rightarrow \) માટે \(i \times \left( {\frac{{{R_2}}}{{{R_1} + {R_2}}}} \right)\)
\( = \frac{{24}}{{23}} \times \left( {\frac{{7.5}}{{2.5 + 7.5}}} \right)\,\, = \,\,\frac{{18}}{{23}}\,A\,\,\,\)
\(\therefore \,\,\,{i_2} = \,\,i - {i_1} = \,\,\frac{{24}}{{23}} - \frac{{18}}{{23}} = \frac{6}{{23}}\,A\)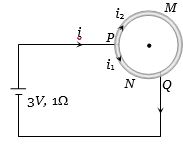
Download our appand get started for free
Similar Questions
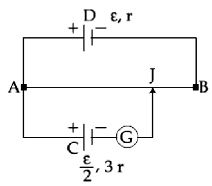
- 1$L$ લંબાઇનો અને $12\, r$ નો અવરોધ ધરાવતા એક પોટેન્શીયોમીટર તાર $AB$ અને $\varepsilon$ જેટલું $emf$ અને $r$ જેટલો આંતરિક અવરોધ ધરાવતા કોષ $D$ સાથે જોડવામાં આવે છે. $\varepsilon/2$ જેટલું $emf$ અને $3r$ જેટલો આતંરિક અવરોધ ધરાવતા કોષ $C$ ને આકૃતિમાં દર્શાવ્યા મુજબ જોડવામાં આવે છે. ગેલ્વેનોમીટરમાં દર્શાવતું શૂન્ય આવર્તન માટેની લંબાઈ $AJ$ _______ હશે.View Solution
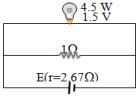
- 2$4.5\, W$, $1.5\, V$ રેટીંગ ધરાવતા બલ્બને આકૃતિમાં દર્શાવ્યા મુજબ લગાડેલ છે. બલ્બને પૂર્ણ પ્રકાશિત કરવા માટે કોષનો $e.m.f$ ................ $V$ હોવો જોઈએ.View Solution
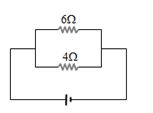
- 3આકૃતિમાં દર્શાવ્યા મુજબ $6\,\Omega$ અવરોધમાં ઉત્પન્ન થતો પાવર $6\ watt$ છે. તો $4\,\Omega$ અવરોધમાં ઉત્પન્ન થતો પાવર .... હશે.View Solution
- 4$20\, \Omega $ સરેરાશ અવરોધ ધરાવતી ઈલેક્ટ્રિક કીટલીમાં $20\,^oC$ તાપમાને રહેલ એક $kg$ પાણી ગરમ કરવામાં આવે છે.મેઇનનો $rms$ વૉલ્ટેજ $200\, V$ છે.કીટલીમાં થતો ઉષ્માનો વ્યયને અવગણતા કિટલીમાં રહેલ પાણીને વરાળમાં ફેરવવા ....... $(\min)$ સમય લાગે? [ પાણીની વિશિષ્ટ ઉષ્મા $= 4200\, J/kg\, ^oC$, પાણીની બાષ્પાયન ગુપ્ત ઉષ્મા $= 2260\, k\,J/kg$]View Solution
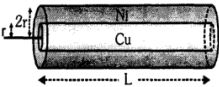
- 5$r$ ત્રિજ્યા અને '$ℓ$' લંબાઈના કોપરના તારને નિકલ પ્લેટ વડે આવરિત કરવામાં આવે છે જ્યાં સુધી તેની ત્રિજ્યા $2r$ બને. જો કોપર અને નિકલની અવરોધકતા $\rho_c$ અને $P_n$ હોય તો તારનો સમતુલ્ય અવરોધ શોધો.View Solution
- 6નીચે બે વિધાન આપેલ છે .View Solution
વિધાન $I:$ $80\; \Omega$ અવરોધ ધરાવતા એક નિયમિત તારને ચાર સમાન ભાગમાં કાપવામાં આવે છે. આ ભાગોને હવે સમાંતરમાં જોડવામાં આવે છે. આ સંયોજની સમતુલ્ય અવરોધ $5 \Omega$ હશે.
વિધાન $II$: બે અવરોધો $2R$ અને $3R$ ને વિદ્યુત પરિપથમાં સમાંતરમાં જોડવામાં આવે છે. $3R$ અને $2R$ માં ઉત્પન્ન થતી ઉષ્મીય ઊર્જાનો ગુણોત્તર $3: 2$ હશે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 7ટંગસ્ટનના અવરોધનો તાપમાન ગુણાંક $4.5 \times 10^{-3}\;{ }^{\circ} C ^{-1}$ અને જર્મેનીયમનો $-5 \times 10^{-2}\;{ }^{\circ} C ^{-1}$ છે. $100 \Omega$ અવરોધના ટંગસ્ટનના તારને $R$ અવરોધના જર્મેનિયમના તાર સાથે શ્રેણીમાં જોડેલ છે, તો $R$ ના $......... \Omega$ મુલ્ય માટે સંયોજનનો અવરોધ તાપમાન સાથે બદલાય નહિં.View Solution
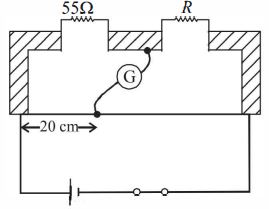
- 8નીચેની આકૃતિમાં ગેલ્વેનોમીટરના શૂન્ય આવર્તન સાથે મીટર બ્રીજ દર્શાવેલ છે. તો અજ્ઞાત-અવરોધ $R$ નું મૂલ્ય ($\Omega$ માં) કેટલું હશે?View Solution
- 9આંતરિક અવરોધ $r$ ધરાવતી બેટરી સાથે $R$ અવરોધ જોડેલ છે $R$ અવરોધ પર મહત્તમ પાવર કરવા માટે ...View Solution
- 10જો $220$ વોલ્ટ $100$ વોટ રેટેડ બલ્બનો બલ્બ વચ્ચેનો વોલ્ટેજ રેટેડ વોલ્ટેજથી $2.5\,\%$ ઘટે છે, તો તેનો પાવર …… $\%$ ઘટશે?View Solution
