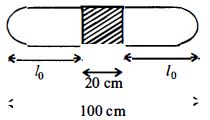
Lengths of \(M\) and \(N\) are \((40-y)\) and \((40+y)\) respecively.
\(P_1=\) Preessure of par \(M\)
\(P_2=\) Pressure of part \(N\)
As temperature is constant
Therefore, we can write \(PV =\) constant
For \(M : P_0(40 A)=P_1(40-y) A\)
\(\Rightarrow P_1=\frac{P_0(40)}{(40-y)} \ldots \ldots .(\text { i })\)
For \(N : P_0(40 A)=P_2(40+y) A\)
\(\Rightarrow P_2=\frac{P_0 40}{(40+y)}\)
Here \(A=\) area of cross section of tube
Pressure at lower face \(\left(P_1\right)=\) Pressure at upper face \(\left(P_2\right)+\) Pressure due to mercury column of height \(20 cm\).
\(P_1=P_2=20 pg\)
Use (i) and (ii) in (iii)
\(P_0 \frac{40}{(40-y)}=\frac{P_0 40}{(40+y)}+20 p g\)
\(\frac{40 P_0}{(40-y)}-\frac{40 P_0}{(40+y)}=20 p g\)
\(40 \times 76 p g\left[\frac{2 y}{1600-y^2}\right]=20 p g\)
\((52)(2 y)=1600-y^2\)
\(304 y=1600-y^2\)
\(y^2+304 y-1600=0\)
Solving for \(y\), we get \(y=5.18\; cm\)
Download our appand get started for free
Similar Questions
- 1$1 \,\mu m$ ત્રિજ્યા ધરાવતું પાણીનું એક ટીપું જ્યાં ઉત્પ્લાવક બળ ના પ્રવર્તતું હોય તેવી જગ્યાએ પડે છે હવા માટે શ્યાનતા ગુણાંક $1.8 \times 10^{-5} \,Nsm ^{-2}$ અને તેની ધનતા પાણીની ધનતા $\left(10^{6} \,gm ^{-3}\right)$ કરતા અવગણી શકાય તેટલી છે. પાણીના ટીપાંનો અન્ય (ટર્મિનલ) વેગ............ $\times 10^{-6}\,ms ^{-1}$ હશે. (ગુરુત્વકર્ષી પ્રવેગ =$10$ $ms$ ${ }^{-2}$ લો.)View Solution
- 2$750 \,kgm ^{-3}$ ની ઘનતા ધરાવતું એક પ્રવાહી એક સમક્ષિતિજ નળી કે જેના એક આડછેદનું ક્ષેત્રફળ $A _{1}=1.2 \times 10^{-2} \,m ^{2}$ અને બીજા ક્ષેત્રનું આડછેદનું ક્ષેત્રફળ $A_{2}=\frac{A_{1}}{2}$ છે, માંથી સરળતાથી વહે છે. નળીના પહોળા અને સાંકળા છેડાઓ વચ્ચે દબાણનો તફાવત $4500 \,Pa$ છે. પ્રવાહીનો વહન દર ............... $\times 10^{-3}\,m ^{3} s ^{-1}$ હશે.View Solution
- 3એક $H$ ઊંચાઈના મોટા પાતને, $\rho$ ઘનતાના પ્રવાહીથી છલોધલ ભરવામાં આવે છે. તેની શિરોલંબ બાજુની સપાટી પર $r$ ત્રિજ્યાનું એક નાનું છિદ્ર બનાવવામાં આવે છે. (તળિયાની એકદમ નજીક) તો પ્રવાહીના દબાણને રોકવા માટે જરરી સમક્ષિતિજ બળ કેટલું હશે ?View Solution
- 4View Solutionએેક બરફ્નો બ્લોક તેલ ભરેલા પાત્રમાં તરી રહ્યો છે, જ્યારે બરફ પીગળી જશે ત્યારે તેલનું સ્તર ...........
- 5$a $ ત્રિજયાની કેશનળી વચ્ચે દબાણનો તફાવત $P $ રાખવાથી પ્રવાહીનો વહન દર $Q$ છે.જો $ a/2 $ ત્રિજયા અને $2P $ દબાણ કરવાથી પ્રવાહીના વહન દર કેટલો થાય?View Solution
- 6View Solutionનળમાંથી પાણી પડે ત્યારે
- 7View Solutionજયારે સિકકો પાણીમાં પડે ત્યારે...
- 8$5\, cm$ ત્રિજ્યા ધરાવતી પાઇપમાથી પાણી $100\,$ લિટર પ્રતિ મિનિટ ના દરથી આવે તો પ્રવાહનો રેનોલ્ડ નંબર કયા ક્રમનો હશે? (પાણીની ઘનતા $= 1000\, kg/m^3$, પાણીનો શ્યાનતાગુણાંક $= 1\, mPa\, s$)View Solution
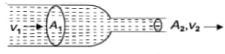
- 9આકૃતિમાં દર્શાવ્યા મુજબ નળીમાં પ્રવાહીનું ડાબી બાજુથી જમણી બાજુ વહન થઈ રહ્યું છે. $A_1$ અને $A_2$ એ દર્શાવ્યા મુજબ નળીના આડછેદના ભાગોનું ક્ષેત્રફળ છે તો ઝડપ $\frac{v_1}{v_2}$ નો ગુણોત્તર ......... હશે ?View Solution
- 10$d _1$ અને $d _2$ ઘનતા ધરાવતા પ્રવાહી એ સમાન દબાણ તફાવત હેઠળ આદર્શ કેપિલરી ટ્યુબમાં વહે છે.પ્રવાહીનું સમાન પ્રમાણ (દળ) વહન કરવા માટે લાગેલો સમય $t _1$ અને $t _2$ હોય, પ્રવાહીના શ્યાનતા ગુણાંકનો ગુણોતર $......... $View Solution
