$100 \Omega$ નો અવરોધ ધરાવતા ગેલ્વેનોમીટરને હ્યારે $400 \Omega$ ના અવરોધ સાથે શ્રેણીમાં જોડવામાં આવે છે ત્યારે $10 \mathrm{~V}$ સુધીનો વૉલ્ટેજ માપે છે . ગેલ્વેનોમીટર ને $10$ $A$ જેટલો પ્રવાહ માપી શકે તેવા એમીટરમાં રૂપાંતારિત કરવા માટેનો જરૂરી અવરોધ $x \times 10^{-2} \Omega$ છે. $x$ નું મૂલ્ય. . . . . . . . હશે.
JEE MAIN 2024, Diffcult
Download our app for free and get started
c
\(\mathrm{i}_{\mathrm{g}}=\frac{10}{400+100}=20 \times 10^{-3} \mathrm{~A}\)
\(\mathrm{i}_{\mathrm{g}}=\frac{10}{400+100}=20 \times 10^{-3} \mathrm{~A}\)
For ammeter
Let shunt resistance \(=\mathrm{S}\)
\(i_g R=\left(i-i_g\right) S\)
\(20 \times 10^{-3} \times 100=10 S\)
\(S=20 \times 10^{-2} \Omega\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જેમાં $I$ જેટલો વિદ્યુતપ્રવાહ વહે છે તેવા એક સુવાહક તારને $N$ આંટા ધરાવતા વર્તુળાકાર ગૂંચળામાં વાળવામાં આવે છે ત્યાર બાદ તેને $n$ આંટા ધરાવતાં વર્તુળાકાર ગૂંચળામાં વાળવામાં આવે છે. બંને ગૂંચળાના કેન્દ્ર આગળ ચુંબકીય ક્ષેત્ર ગણવામાં આવે છે. પ્રથમ કિસ્સામાં અને બીજા કિસ્સામાં મળતા ચુંબકીય ક્ષેત્રનો ગુણોતર $.............$ થશે.View Solution
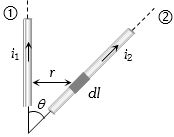
- 2તાર $1$ અને $2$ માંથી $ {i_1} $ અને $ {i_2} $ પ્રવાહ પસાર થાય છે.તાર $2$ નો ખંડ $dl$ તાર $1$ થી $r$ અંતરે છે,તો ખંડ પર કેટલું બળ લાગશે?View Solution
- 3$R$ ત્રિજયા ધરાવતી રીંગ પરના $A$ અને $B$ બિંદુ વચ્ચે બેટરી લગાવેલ છે. $AB$ એ કેન્દ્ર આગળ $ \theta $ ખૂણો બનાવે છે.તો કેન્દ્ર પર ચુંબકીયક્ષેત્ર...View Solution
- 4$n$ આંટાવાળી અને $2l$ બાજુવાળી ચોરસફ્રેમના કેન્દ્ર પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 5$4.0\, cm$ અંતરે રહેલા, બે લાંબા સીધા અને સમાંતર તાર $A$ અને $B$ માંથી $8.0 \,A$ અને $5.0\, A$ વિદ્યુતપ્રવાહો એક જ (સમાન) દિશામાં વહે છે. તાર ના $10 \,cm$ લંબાઈના વિભાગ પર લાગતું બળ શોધોView Solution
- 6$m$ ચુંબકીય મોમેન્ટ ધરાવતી એક ચોરસ લૂપમાં $I$ જેટલો સ્થિર પ્રવાહ વહે છે જો આ ચોરસ લૂપને વર્તુળાકાર લૂપમાં ફેરવવામાં આવે અને તેમાથી સમાન પ્રવાહ વહે છે.આ વર્તુળાકાર લૂપની ચુંબકીય મોમેન્ટ નું મૂલ્ય કેટલું થશે?View Solution
- 7$2 \mathrm{~m}$ લંબાઈ ની બાજુ અને $2 \mathrm{~A}$ પ્રવાહ ધરાવતા એક ચોરસ ગાળાને તેની બાજુઓ $x-y$ અક્ષને સમાંતર રહે તે રીતે મૂકેલ છે. ક્ષેત્ર $x-1$ સમતલમાંથી ચુંબકીય પસાર થાય છે અને તે $\vec{B}=B_0(1+4 x) \hat{\mathrm{k}}$, જ્યાં $B_0=5$ ટેસલા વડે રજૂ થાય છે. ગાળા દ્વારા અનુભવાતું પરિણ઼ામી ચુંબકીય બળ ............... $\mathrm{N}$ છે.View Solution
- 8એક વર્તુળાકાર વિદ્યુતપ્રવાહધારિત ગુંચળાની ત્રિજ્યા $R$ છે. ગુંચળાના કેન્દ્રથી તેની અક્ષ પર કેટલા અંતરે ચુંબકીયક્ષેત્રની તીવ્રતા તેના કેન્દ્ર પરની તીવ્રતા કરતા $\frac{1}{2 \sqrt{2}}$ ગણી હશે?View Solution
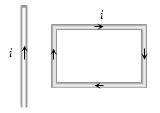
- 9View Solutionચોરસ ફ્રેમ કઇ બાજુ ગતિ કરશે?
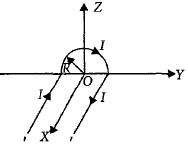
- 10આકૃતિમાં દર્શાવ્યા અનુસારના તારના આકારમાંથી $I$ પ્રવાહ પસાર થાય છે. તારનો સુરેખ ભાગ ઘણો લાંબો અને $ X-$ અક્ષને સમાંતર છે, જયારે અર્ધવર્તુળાકાર ભાગની ત્રિજયા $R$ છે જે $Y-Z$ સમતલમાં છે. $O$ બિંદુ આગળ ચુંબકીયક્ષેત્ર કેટલું મળે?View Solution
